Current state of R packages for the design of experiments

experimental design
R

Your analytical toolkit matters very little if the data are no good. Ideally you want to know to how the data were collected before delving into the analysis of the data; better yet, get involved before the collection of data and design its collection. In this post I explore some of the top downloaded R packages for the design of experiments and analysis of experimental data.

Author
Affiliation
Emi Tanaka

Monash University

Published

February 3, 2021

library(tidyverse)
── Attaching packages ─────────────────────────────────────── tidyverse 1.3.1 ──
✔ ggplot2 3.3.6     ✔ purrr   0.3.4
✔ tibble  3.1.8     ✔ dplyr   1.0.9
✔ tidyr   1.2.0     ✔ stringr 1.4.0
✔ readr   2.1.2     ✔ forcats 0.5.1
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag()    masks stats::lag()
library(rvest)

Attaching package: 'rvest'
The following object is masked from 'package:readr':

    guess_encoding
library(lubridate)

Attaching package: 'lubridate'
The following objects are masked from 'package:base':

    date, intersect, setdiff, union
library(cranlogs)
library(glue)
library(scales)

Attaching package: 'scales'
The following object is masked from 'package:purrr':

    discard
The following object is masked from 'package:readr':

    col_factor
library(colorspace)
library(tidytext)
library(pluralize)
library(kableExtra)

Attaching package: 'kableExtra'
The following object is masked from 'package:dplyr':

    group_rows
library(igraph)

Attaching package: 'igraph'
The following objects are masked from 'package:lubridate':

    %--%, union
The following objects are masked from 'package:dplyr':

    as_data_frame, groups, union
The following objects are masked from 'package:purrr':

    compose, simplify
The following object is masked from 'package:tidyr':

    crossing
The following object is masked from 'package:tibble':

    as_data_frame
The following objects are masked from 'package:stats':

    decompose, spectrum
The following object is masked from 'package:base':

    union
library(ggraph)

myggtheme <- 
  theme(panel.background = element_rect(fill = NA),
        panel.grid = element_line(color = "#f6e5ee"),
        axis.text = element_text(color = "#79003e"),
        axis.line = element_line(color = "#79003e", size = 0.7),
        axis.ticks.length = unit(1.4, "mm"),
        axis.ticks = element_line(color = "#79003e", size = 0.7),
        axis.title = element_text(color = "#79003e", face = "bold"),
        strip.background = element_rect(color = "#79003e",
                                        fill = "#AD0059"),
        strip.text = element_text(color = "white"),
        plot.title.position = "plot",
        plot.title = element_text(color = "#79003e", face = "bold")) 
# Thanks to Dirk Eddelbuettel's answer on SO:
# https://stackoverflow.com/questions/11560865/list-and-description-of-all-packages-in-cran-from-within-r
url <-  "https://cran.rstudio.com/web/packages/packages.rds"
db <- readRDS(url(url)) %>% 
  as.data.frame()
nanalysis <- db %>% 
  filter(str_detect(tolower(Title), "analysis")) %>% 
  nrow()

ndesign <- db %>% 
  filter(str_detect(tolower(Title), "design")) %>% 
  nrow()

Data collection

As many know, it doesn’t matter how good your analytical tools is if your data are rubbish. This sentiment is often captured in the expression “garbage in, garbage out”. It’s something we all seem to know but there is still a tendency for many of us to place a greater focus on the analysis1. This is perhaps all natural given that a potential for discovery is just so much more exciting than ensuring the quality of the collected data.

So what is considered as good quality data? A lack of error in the data? Data containing enough range of variables and sample size for the downstream analysis? Giving an explicit definition of a good quality data is a fraught exercise, but if you know how the data were collected then you can better perform the initial data analysis (Chatfield 1985) to weed out (or fix) potential poor quality data. This step will likely get more value out of the data than fitting complex models to poor quality data.

Better than knowing how the data were collected, if you can design the collection of data so that it’s optimised for the purpose of the analysis2, then you can potentially get even a better value out of your data. Not all data collection starts with an explicit analytical plan though. Furthermore, you may have very little control of how the data are collected. Often these are observational data or making a secondary use of experimental data. This article will focus on data collection of an experiment where you have some control of the collection process.

Experimental data

All experiments are conducted with some objective in mind. This could be that a scientist may wish to test their hypothesis, a manufacturer wants to know which manufacturing process is better or a researcher wants to understand some cause-and-effect relationships. A characteristic part of an experiment is that the experimenter has control over some explanatory variables. In a comparative experiment, the control is over the allocation of treatments to subjects. Designing an experiment in the statistics discipline usually focus on this allocation, although it’s important to keep in mind that there are other decision factors in an experiment.

Data that are collected from experiments are what we refer to as experimental data. Because it was collected with some objective in mind followed by some data collection plan, experimental data are often thought of to be better quality than observational data. But then again if you can’t quantify the quality of data, you can’t really tell. Certain scientific claims (e.g. causation, better treatment) can only be substantiated by experiments and so experimental data is held to a higher standard in general.

Design and analysis of experiments

dat_DoE <- read_html("https://cran.r-project.org/web/views/ExperimentalDesign.html")
date_download <- Sys.Date()
cran_names <- available.packages(repos = "https://cran.rstudio.com/") %>% 
  rownames() %>% 
  unique() # it should be unique
doe_pkgs <- dat_DoE %>% 
  html_nodes("li") %>% 
  html_nodes("a") %>% 
  html_text() %>% 
  .[. %in% cran_names] %>% 
  unique()

dat_survey <- read_html("https://cran.r-project.org/web/views/OfficialStatistics.html")
survey_pkgs <- dat_survey %>% 
  html_nodes("li") %>% 
  html_nodes("a") %>% 
  html_text() %>% 
  .[. %in% cran_names] %>% 
  unique()

There are all together 83 R-packages in the CRAN Task View of Design of Experiments & Analysis of Experimental Data as of 2022-09-18.3 I’m going to refer these packages as DoE packages, although there are some packages in the mix that are more about the analysis of experimental data rather than the design of experiments and there are some packages that are missing in the list (e.g. DeclareDesign). The DoE packages make up about 0.4% of the 18,592 packages available in CRAN.

The DoE packages don’t include survey design. These instead belong to the CRAN Task View of Official Statistics & Survey Methodology which contains 122 packages. While some surveys are part of an experimental study, most often they generate observational data.

Below I have a number of different analysis for these DoE packages. If you push the button on the top right corner of this article, you can toggle the display for the code or alternatively you can have a look at the source Rmd document.

Bigram of DoE package titles and descriptions

stop_words_ext <- c(stop_words$word, "doi")

doe_db <- db %>% 
  filter(Package %in% doe_pkgs) %>% 
  mutate(Description = str_replace_all(Description, "\n", " "),
         Description = str_squish(Description),
         Title = str_replace_all(Title, "\n", " "))

bigram_tab <- function(data, col) {
  data %>% 
    unnest_tokens(word, {{col}}, token = "ngrams", n = 2) %>% 
    separate(word, c("word1", "word2"), sep = " ") %>% 
    mutate(word1 = singularize(word1),
           word2 = singularize(word2)) %>% 
    # don't count the same bigram within the same package
    distinct(Package, word1, word2) %>% 
    filter(!word1 %in% stop_words_ext,
           !word2 %in% stop_words_ext,
           !str_detect(word1, "^[0-9.]+$"),
           !str_detect(word2, "^[0-9.]+$")) %>% 
    count(word1, word2, sort = TRUE)  
}
bigram_tab(doe_db, Description) %>% 
  filter(n > 4) %>% 
  mutate(word = paste(word1, word2)) %>% 
  select(word, n) %>% 
  kbl(caption = "The bigram of the R-package _descriptions_ as provided in the DESCRIPTION file in CRAN.", 
               col.names = c("Bigram", "Count")) %>% 
  kable_classic(full_width = FALSE)
bigram_tab(doe_db, Title) %>% 
  filter(n > 3) %>% 
  mutate(word = paste(word1, word2)) %>% 
  select(word, n) %>% 
  kbl(caption = "The bigram of the R-package _titles_ as provided in the DESCRIPTION file in CRAN.", 
               col.names = c("Bigram", "Count")) %>% 
  kable_classic(full_width = FALSE)

Table @ref(tab:bigram-title) shows the most common bigrams in the title of the DoE packages. It’s perhaps not surprising but the words “optimal design” and “experimental design” are the top. It’s also likely that the words “design of experiments” appears often but because this is a bigram (two consecutive words) so it doesn’t appear. You might then wonder if that’s the case words like “design of” or “of experiments” should make an appearance, however “of” is a stop word and these are filtered out otherwise unwanted bigrams come up on the top.

There are couple of words like “clinical trial” and “dose finding” that suggests applications in medical experiments, as well as “microarray experiment” that suggests application in bioinformatics.

The bigram of the R-package _titles_ as provided in the DESCRIPTION file in CRAN.
Bigram Count
experimental design 6
optimal design 6
clinical trial 5
dose finding 5
sequential design 5
block design 4
microarray experiment 4

The title alone might be too succinct for text analysis so I also had a look at the most common bigrams in the description of the DoE packages as shown in Table @ref(tab:bigram-desc). The counts in Table @ref(tab:bigram-desc) (and also Table @ref(tab:bigram-title)) is across the DoE packages. To be more clear, even if the bigram is mentioned multiple times within the description, it’s only counted once per package. This removes the inflation of the counts due to one package mentioning the same bigram over and over again.

Again not surprisingly “experimental design” and “optimal design” comes on top in the DoE package descriptions. The words “graphical user” and “user interface” implies that the trigram “graphical user interface” was probably common.

The bigram of the R-package _descriptions_ as provided in the DESCRIPTION file in CRAN.
Bigram Count
experimental design 7
optimal design 7
block design 5
clinical trial 5
factorial design 5
graphical user 5
microarray experiment 5
user interface 5

Network of DoE package imports and dependencies

doe_imports <- doe_db %>% 
  mutate(Depends = str_replace_all(Depends, "\n", " "),
         Depends = str_replace_all(Depends, fixed("("), " ("),
         Imports = str_replace_all(Imports, "\n", " "),
         Imports = str_replace_all(Imports, fixed("("), " ("),
         imports = str_c(Depends, Imports, sep = ","),
         imports = str_split(imports, ","),
         imports = map(imports, ~{
                    str_squish(.x) %>% 
                      word() %>% 
                      .[.!=""]}
           ),
         imports_doe = map(imports, ~.x[.x %in% doe_pkgs])) %>% 
  select(Package, imports_doe) %>% 
  unnest_longer(imports_doe) %>% 
  filter(!is.na(imports_doe)) %>% 
  rename(from = imports_doe, to = Package) %>% 
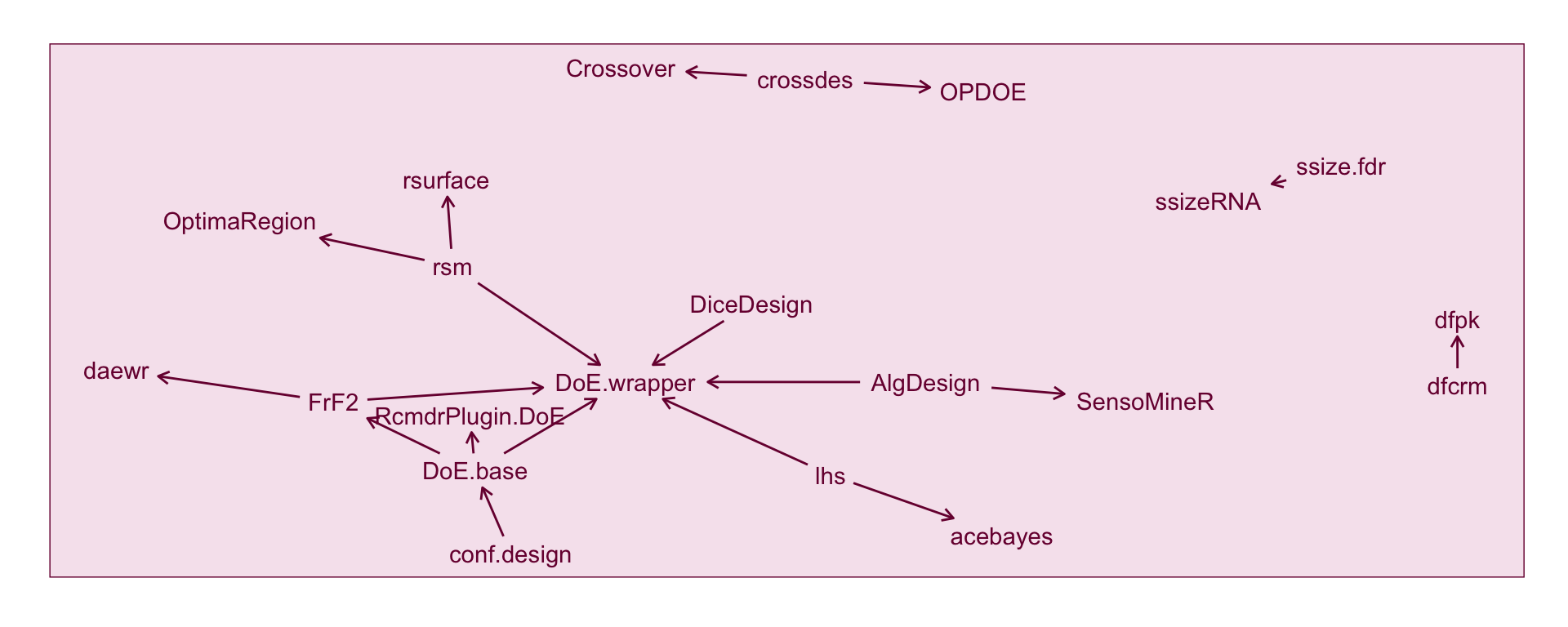
  select(from, to)

Figure @ref(fig:doe-network) shows the imports and dependency between the DoE packages. We can see here that DoE.wrapper imports a fair number of DoE packages that results in the major network cluster see in Figure @ref(fig:doe-network). AlgDesign and DoE.base are imported into four other DoE packages so form an important base in the DoE world.

graph_from_data_frame(doe_imports) %>% 
  ggraph(layout = 'fr') +
  geom_edge_link(aes(start_cap = label_rect(node1.name),
                     end_cap = label_rect(node2.name)), 
                 arrow = arrow(length = unit(2, 'mm')),
                 color = "#79003e") + 
  geom_node_text(aes(label = name),
                 color = "#79003e") +
  theme(panel.background = element_rect(fill = "#f6e5ee",
                                        color = "#79003e"),
        plot.margin = margin(20, 20, 20, 20))

(ref:network) The network of imports and dependency among DoE packages alone. Each node represents a DoE package. DoE packages with no imports or dependency on other DoE packages are excluded. Each arrow represents the relationship between the packages such that the package on the tail is used by package on the head of the arrow.

(ref:network)

CRAN download logs

end <- Sys.Date() - 2 # usually 1-2 days are not available yet
start <- end - years(5) + days(2)
dldat <- cran_downloads(doe_pkgs, from = start, to = end)
dldat %>% 
    group_by(package) %>% 
    summarise(total = sum(count)) %>%
  ggplot(aes(total)) + 
  geom_histogram(color = "white", fill = "#AD0059") + 
  scale_x_log10(label = comma) + 
  myggtheme + 
  labs(x = glue("Total download counts from {start} to {end}"),
       y = "Number of packages") +
  scale_y_continuous(expand = c(0, 0))

Figure @ref(fig:download-hist) shows the distribution of the total download counts over the last 5 years4 of the DoE packages. This graph doesn’t take into account that some DoE packages may only have been on CRAN in the last 5 years so the counts are in favour of DoE packages that’s been on CRAN longer.

(ref:hist) Histogram of the total download count over last 5 years of the DoE packages.

`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.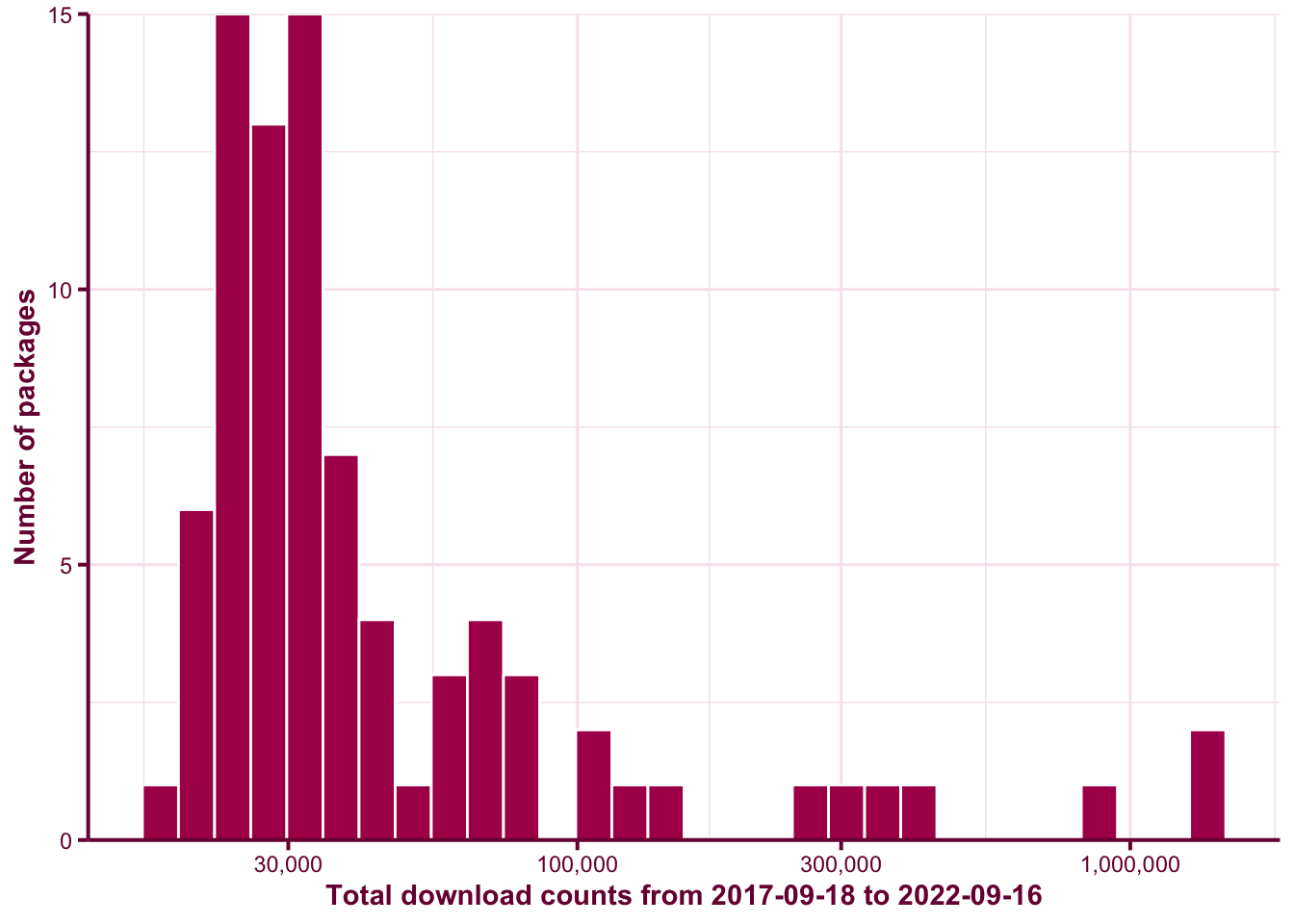

(ref:hist)

Top 5 DoE packages

ntop <- 5

top5sum_df <- dldat %>% 
  group_by(package) %>% 
  summarise(total = sum(count)) %>% 
  ungroup() %>% 
  slice_max(order_by = total, n = ntop)

top5 <- top5sum_df %>% 
  pull(package) 

top5_df <- dldat %>% 
  filter(package %in% top5) %>% 
  mutate(package = fct_reorder(package, count, function(x) -sum(x)))

The top 5 downloaded DoE packages at the time of this writing are AlgDesign, lhs, DiceDesign, DoE.base, and FrF2. You can see the download counts in Figure @ref(fig:download-barplot).

top5sum_df %>% 
  mutate(package = fct_reorder(package, total)) %>% 
  ggplot(aes(total, package)) +
  geom_col(aes(fill = package)) +
  labs(x = glue("Total downloads from {start} to {end}"),
       y = "Package") + 
  scale_x_continuous(labels = comma, expand = c(0, 0)) +
  myggtheme + 
  scale_fill_discrete_qualitative(rev = TRUE) + 
  guides(fill = FALSE)

(ref:barplot) The above barplot shows the total downloads of the top 5 downloaded DoE packages from the period 2017-09-18 to 2022-09-16.

Warning: `guides(<scale> = FALSE)` is deprecated. Please use `guides(<scale> =
"none")` instead.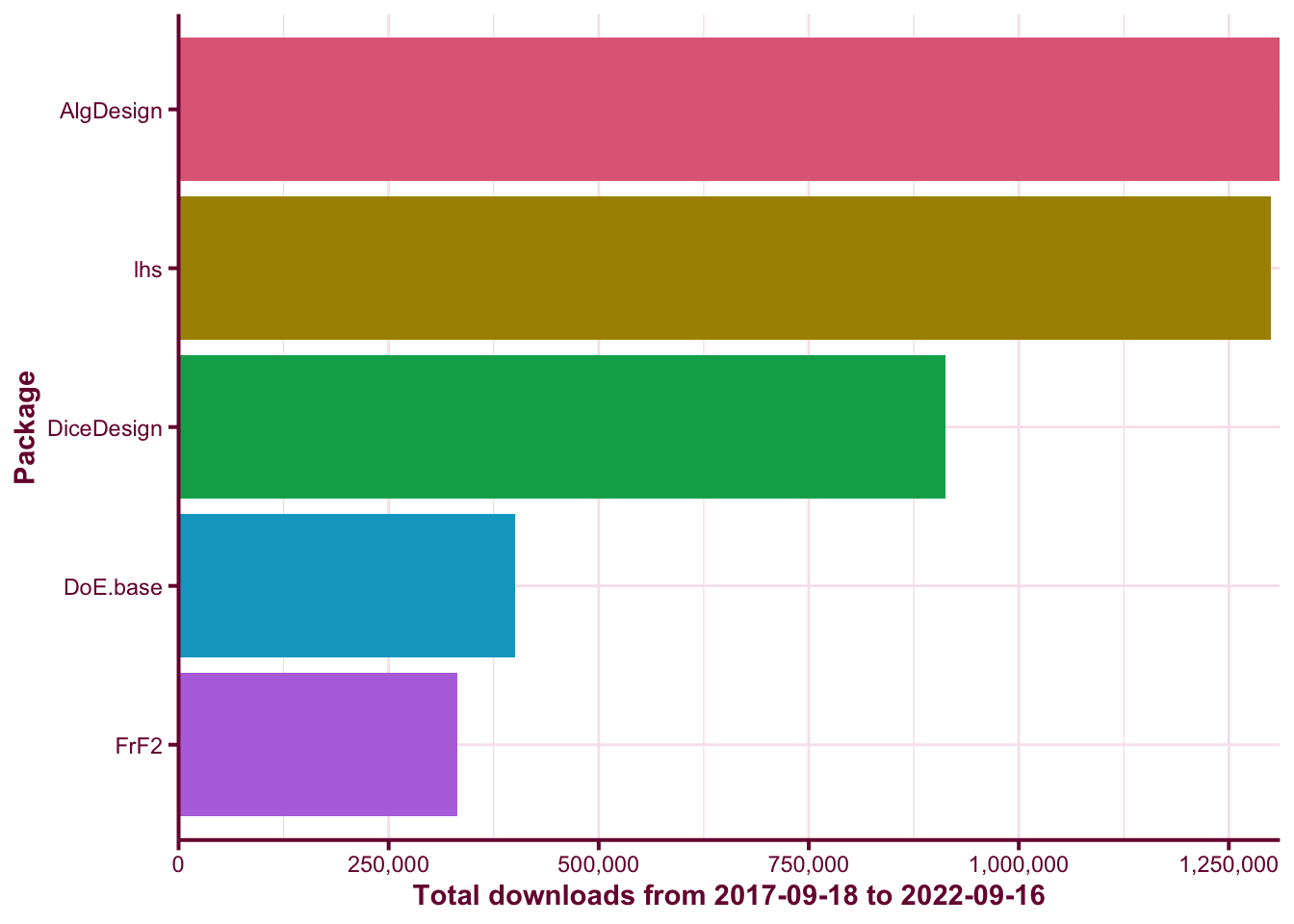

(ref:barplot)

We can have a look at further examination of the top 5 DoE packages by looking at the daily download counts as shown in Figure @ref(fig:download-barplot). The download counts are the raw values and these include downloads by CRAN mirror and bots. There is a noticeable spike when there is an update to the CRAN package. This is partly because when there is a new version of the package, when you install other packages that depend or import it then R will prompt you to install the new version. This means that the download counts are inflated and to some extent you can artificially boost them by making regular CRAN updates. The adjustedcranlogs (Morgan-Wall 2017) makes a nice attempt to adjust the raw counts based on a certain heuristic. I didn’t use it since the adjustment is stochastic and I appear to have hit a bug.

pkg_url <- "https://cran.r-project.org/web/packages/{pkg}/index.html"
pkg_archive <- "https://cran.r-project.org/src/contrib/Archive/{pkg}/"
pkg_updates <- map(top5, function(pkg) {
    last_update <- read_html(glue(pkg_url)) %>% 
      html_table() %>% 
      .[[1]] %>% 
      filter(X1=="Published:") %>% 
      pull(X2) %>% 
      ymd()
      
    archive_dates <- tryCatch({ 
        read_html(glue(pkg_archive)) %>% 
          html_table() %>%
          .[[1]] %>% 
          pull(`Last modified`) %>% 
          ymd_hm() %>% 
          na.omit() %>% 
          as.Date()
      }, error = function(e) {
        NULL
      })
    c(archive_dates, last_update)
  })
names(pkg_updates) <- top5

updates <- unlist(pkg_updates) %>% 
  enframe("package", "update") %>% 
  # unlist converts date to integers
  mutate(update = as.Date(update, origin = "1970-01-01"),
         # need to get rid of the numbers appended to pkg names
         package = str_extract(package, paste0(top5, collapse="|")),
         package = factor(package, levels = top5)) %>% 
  filter(between(update, start, end))
ggplot(top5_df, aes(date, count, color = package)) +
  # add shadow lines
  geom_line(data = rename(top5_df, package2 = package), 
            color = "gray", aes(group = package2)) +
  # add date when package was updated
  geom_vline(data = updates, aes(xintercept = update),
             linetype = "dashed", color = "#79003e") + 
  # the trend line
  geom_line() +
  scale_y_log10() +
  facet_grid(package ~ .) + 
  labs(title = glue("Top 5 downloaded DoE packages from {start} to {end}")) + 
  scale_color_discrete_qualitative() +
  guides(color = FALSE) +
  myggtheme

(ref:timeplot) The above plot shows the daily downloads of the top 5 downloaded DoE packages from the period 2017-09-18 to 2022-09-16. The vertical dotted bar corresponds to the date that a new version of the corresponding package was released on CRAN.

Warning: `guides(<scale> = FALSE)` is deprecated. Please use `guides(<scale> =
"none")` instead.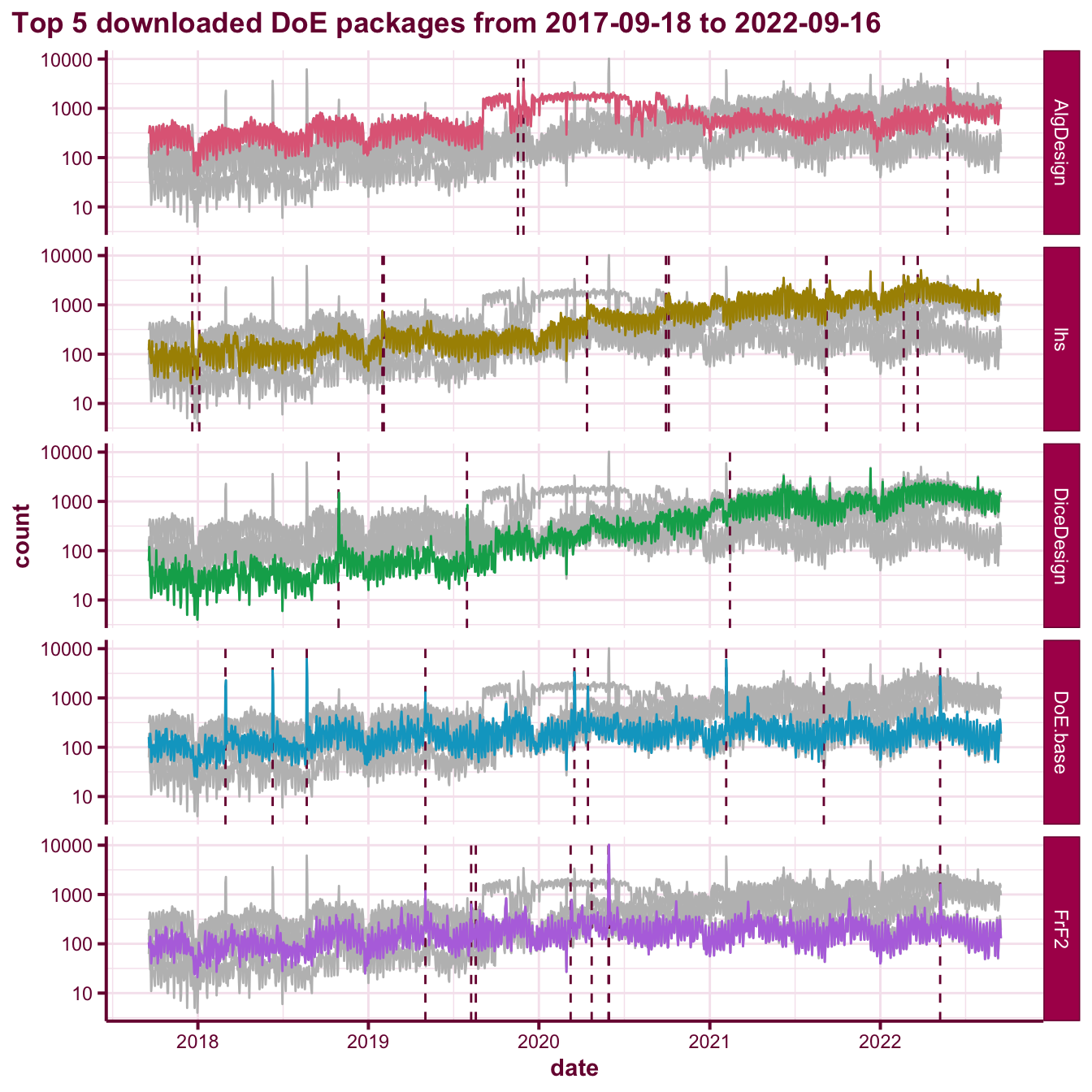

(ref:timeplot)

R-packages

Here we have a closer look at the functions of the top 5 downloaded DoE packages below ordered by their download counts.

  1. AlgDesign CRAN GitHub Wheeler (2019)
    Algorithmic Experimental Design
    Originally written by Bob Wheeler but Jerome Braun have taken over maintenance of the package.
  2. agricolae CRAN de Mendiburu (2020)
    Statistical Procedures for Agricultural Research
    Written and maintained by Felipe de Mendiburu
  3. lhs CRAN GitHub Carnell (2020)
    Latin Hypercube Samples
    Written and maintained by Rob Carnell
  4. ez CRAN GitHub Lawrence (2016)
    Easy Analysis and Visualization of Factorial Experiments
    Written and maintained by Michael A. Lawrence
  5. DoE.base CRAN Grömping (2018)
    Full Factorials, Orthogonal Arrays and Base Utilities for DoE Packages
    Written and maintained by Ulrike Groemping.

Before we look at the packages, let’s set a seed so we can reproduce the results.

set.seed(2021)

AlgDesign

To start off, we begin with the most downloaded DoE package, AlgDesign. The examples below are taken directly from the vignette of the AlgDesign package.

library(AlgDesign)

You can create a balanced incomplete block design using the optBlock function. It’s using an optimal design framework where the default criterion is D criterion and the implied model is given in the first argument.

BIB <- optBlock(~ ., 
                withinData = factor(1:7), 
                blocksize = rep(3, 7))
BIB
$D
[1] 0.08033556

$diagonality
[1] 0.692

$Blocks
$Blocks$B1
  X1
1  1
3  3
4  4

$Blocks$B2
  X1
2  2
4  4
5  5

$Blocks$B3
  X1
4  4
6  6
7  7

$Blocks$B4
  X1
3  3
5  5
6  6

$Blocks$B5
  X1
2  2
3  3
7  7

$Blocks$B6
  X1
1  1
2  2
6  6

$Blocks$B7
  X1
1  1
5  5
7  7


$design
   X1
1   1
3   3
4   4
2   2
41  4
5   5
42  4
6   6
7   7
31  3
51  5
61  6
21  2
32  3
71  7
11  1
22  2
62  6
12  1
52  5
72  7

$rows
 [1] 1 3 4 2 4 5 4 6 7 3 5 6 2 3 7 1 2 6 1 5 7

AlgDesign also includes helper functions to generate a factorial structure.

dat <- gen.factorial(2, 7)
dat
    X1 X2 X3 X4 X5 X6 X7
1   -1 -1 -1 -1 -1 -1 -1
2    1 -1 -1 -1 -1 -1 -1
3   -1  1 -1 -1 -1 -1 -1
4    1  1 -1 -1 -1 -1 -1
5   -1 -1  1 -1 -1 -1 -1
6    1 -1  1 -1 -1 -1 -1
7   -1  1  1 -1 -1 -1 -1
8    1  1  1 -1 -1 -1 -1
9   -1 -1 -1  1 -1 -1 -1
10   1 -1 -1  1 -1 -1 -1
11  -1  1 -1  1 -1 -1 -1
12   1  1 -1  1 -1 -1 -1
13  -1 -1  1  1 -1 -1 -1
14   1 -1  1  1 -1 -1 -1
15  -1  1  1  1 -1 -1 -1
16   1  1  1  1 -1 -1 -1
17  -1 -1 -1 -1  1 -1 -1
18   1 -1 -1 -1  1 -1 -1
19  -1  1 -1 -1  1 -1 -1
20   1  1 -1 -1  1 -1 -1
21  -1 -1  1 -1  1 -1 -1
22   1 -1  1 -1  1 -1 -1
23  -1  1  1 -1  1 -1 -1
24   1  1  1 -1  1 -1 -1
25  -1 -1 -1  1  1 -1 -1
26   1 -1 -1  1  1 -1 -1
27  -1  1 -1  1  1 -1 -1
28   1  1 -1  1  1 -1 -1
29  -1 -1  1  1  1 -1 -1
30   1 -1  1  1  1 -1 -1
31  -1  1  1  1  1 -1 -1
32   1  1  1  1  1 -1 -1
33  -1 -1 -1 -1 -1  1 -1
34   1 -1 -1 -1 -1  1 -1
35  -1  1 -1 -1 -1  1 -1
36   1  1 -1 -1 -1  1 -1
37  -1 -1  1 -1 -1  1 -1
38   1 -1  1 -1 -1  1 -1
39  -1  1  1 -1 -1  1 -1
40   1  1  1 -1 -1  1 -1
41  -1 -1 -1  1 -1  1 -1
42   1 -1 -1  1 -1  1 -1
43  -1  1 -1  1 -1  1 -1
44   1  1 -1  1 -1  1 -1
45  -1 -1  1  1 -1  1 -1
46   1 -1  1  1 -1  1 -1
47  -1  1  1  1 -1  1 -1
48   1  1  1  1 -1  1 -1
49  -1 -1 -1 -1  1  1 -1
50   1 -1 -1 -1  1  1 -1
51  -1  1 -1 -1  1  1 -1
52   1  1 -1 -1  1  1 -1
53  -1 -1  1 -1  1  1 -1
54   1 -1  1 -1  1  1 -1
55  -1  1  1 -1  1  1 -1
56   1  1  1 -1  1  1 -1
57  -1 -1 -1  1  1  1 -1
58   1 -1 -1  1  1  1 -1
59  -1  1 -1  1  1  1 -1
60   1  1 -1  1  1  1 -1
61  -1 -1  1  1  1  1 -1
62   1 -1  1  1  1  1 -1
63  -1  1  1  1  1  1 -1
64   1  1  1  1  1  1 -1
65  -1 -1 -1 -1 -1 -1  1
66   1 -1 -1 -1 -1 -1  1
67  -1  1 -1 -1 -1 -1  1
68   1  1 -1 -1 -1 -1  1
69  -1 -1  1 -1 -1 -1  1
70   1 -1  1 -1 -1 -1  1
71  -1  1  1 -1 -1 -1  1
72   1  1  1 -1 -1 -1  1
73  -1 -1 -1  1 -1 -1  1
74   1 -1 -1  1 -1 -1  1
75  -1  1 -1  1 -1 -1  1
76   1  1 -1  1 -1 -1  1
77  -1 -1  1  1 -1 -1  1
78   1 -1  1  1 -1 -1  1
79  -1  1  1  1 -1 -1  1
80   1  1  1  1 -1 -1  1
81  -1 -1 -1 -1  1 -1  1
82   1 -1 -1 -1  1 -1  1
83  -1  1 -1 -1  1 -1  1
84   1  1 -1 -1  1 -1  1
85  -1 -1  1 -1  1 -1  1
86   1 -1  1 -1  1 -1  1
87  -1  1  1 -1  1 -1  1
88   1  1  1 -1  1 -1  1
89  -1 -1 -1  1  1 -1  1
90   1 -1 -1  1  1 -1  1
91  -1  1 -1  1  1 -1  1
92   1  1 -1  1  1 -1  1
93  -1 -1  1  1  1 -1  1
94   1 -1  1  1  1 -1  1
95  -1  1  1  1  1 -1  1
96   1  1  1  1  1 -1  1
97  -1 -1 -1 -1 -1  1  1
98   1 -1 -1 -1 -1  1  1
99  -1  1 -1 -1 -1  1  1
100  1  1 -1 -1 -1  1  1
101 -1 -1  1 -1 -1  1  1
102  1 -1  1 -1 -1  1  1
103 -1  1  1 -1 -1  1  1
104  1  1  1 -1 -1  1  1
105 -1 -1 -1  1 -1  1  1
106  1 -1 -1  1 -1  1  1
107 -1  1 -1  1 -1  1  1
108  1  1 -1  1 -1  1  1
109 -1 -1  1  1 -1  1  1
110  1 -1  1  1 -1  1  1
111 -1  1  1  1 -1  1  1
112  1  1  1  1 -1  1  1
113 -1 -1 -1 -1  1  1  1
114  1 -1 -1 -1  1  1  1
115 -1  1 -1 -1  1  1  1
116  1  1 -1 -1  1  1  1
117 -1 -1  1 -1  1  1  1
118  1 -1  1 -1  1  1  1
119 -1  1  1 -1  1  1  1
120  1  1  1 -1  1  1  1
121 -1 -1 -1  1  1  1  1
122  1 -1 -1  1  1  1  1
123 -1  1 -1  1  1  1  1
124  1  1 -1  1  1  1  1
125 -1 -1  1  1  1  1  1
126  1 -1  1  1  1  1  1
127 -1  1  1  1  1  1  1
128  1  1  1  1  1  1  1

This can be an input to specify the design using another function, say with optFederov which uses Federov’s exchange algorithm to generate the design.

desF <- optFederov(~ .^2, 
                   data = dat,
                   nTrials = 32,
                   nRepeats = 100)
desF
$D
[1] 0.8867999

$A
[1] 1.296784

$Ge
[1] 0.412

$Dea
[1] 0.241

$design
    X1 X2 X3 X4 X5 X6 X7
4    1  1 -1 -1 -1 -1 -1
5   -1 -1  1 -1 -1 -1 -1
10   1 -1 -1  1 -1 -1 -1
11  -1  1 -1  1 -1 -1 -1
16   1  1  1  1 -1 -1 -1
17  -1 -1 -1 -1  1 -1 -1
23  -1  1  1 -1  1 -1 -1
28   1  1 -1  1  1 -1 -1
30   1 -1  1  1  1 -1 -1
33  -1 -1 -1 -1 -1  1 -1
38   1 -1  1 -1 -1  1 -1
44   1  1 -1  1 -1  1 -1
50   1 -1 -1 -1  1  1 -1
51  -1  1 -1 -1  1  1 -1
56   1  1  1 -1  1  1 -1
61  -1 -1  1  1  1  1 -1
66   1 -1 -1 -1 -1 -1  1
67  -1  1 -1 -1 -1 -1  1
72   1  1  1 -1 -1 -1  1
76   1  1 -1  1 -1 -1  1
77  -1 -1  1  1 -1 -1  1
84   1  1 -1 -1  1 -1  1
86   1 -1  1 -1  1 -1  1
90   1 -1 -1  1  1 -1  1
95  -1  1  1  1  1 -1  1
100  1  1 -1 -1 -1  1  1
105 -1 -1 -1  1 -1  1  1
110  1 -1  1  1 -1  1  1
111 -1  1  1  1 -1  1  1
117 -1 -1  1 -1  1  1  1
123 -1  1 -1  1  1  1  1
128  1  1  1  1  1  1  1

$rows
 [1]   4   5  10  11  16  17  23  28  30  33  38  44  50  51  56  61  66  67  72
[20]  76  77  84  86  90  95 100 105 110 111 117 123 128

If you want to further randomise within blocks, you can pass the above result to optBlock.

desFBlk <- optBlock(~ .^2, 
                    withinData = desF$design,
                    blocksizes = rep(8, 4),
                    nRepeats = 20)

desFBlk
$D
[1] 0.8049815

$diagonality
[1] 0.836

$Blocks
$Blocks$B1
    X1 X2 X3 X4 X5 X6 X7
4    1  1 -1 -1 -1 -1 -1
17  -1 -1 -1 -1  1 -1 -1
23  -1  1  1 -1  1 -1 -1
33  -1 -1 -1 -1 -1  1 -1
77  -1 -1  1  1 -1 -1  1
84   1  1 -1 -1  1 -1  1
90   1 -1 -1  1  1 -1  1
123 -1  1 -1  1  1  1  1

$Blocks$B2
    X1 X2 X3 X4 X5 X6 X7
10   1 -1 -1  1 -1 -1 -1
16   1  1  1  1 -1 -1 -1
28   1  1 -1  1  1 -1 -1
50   1 -1 -1 -1  1  1 -1
61  -1 -1  1  1  1  1 -1
67  -1  1 -1 -1 -1 -1  1
86   1 -1  1 -1  1 -1  1
100  1  1 -1 -1 -1  1  1

$Blocks$B3
    X1 X2 X3 X4 X5 X6 X7
5   -1 -1  1 -1 -1 -1 -1
11  -1  1 -1  1 -1 -1 -1
30   1 -1  1  1  1 -1 -1
44   1  1 -1  1 -1  1 -1
56   1  1  1 -1  1  1 -1
66   1 -1 -1 -1 -1 -1  1
95  -1  1  1  1  1 -1  1
110  1 -1  1  1 -1  1  1

$Blocks$B4
    X1 X2 X3 X4 X5 X6 X7
38   1 -1  1 -1 -1  1 -1
51  -1  1 -1 -1  1  1 -1
72   1  1  1 -1 -1 -1  1
76   1  1 -1  1 -1 -1  1
105 -1 -1 -1  1 -1  1  1
111 -1  1  1  1 -1  1  1
117 -1 -1  1 -1  1  1  1
128  1  1  1  1  1  1  1


$design
    X1 X2 X3 X4 X5 X6 X7
4    1  1 -1 -1 -1 -1 -1
17  -1 -1 -1 -1  1 -1 -1
23  -1  1  1 -1  1 -1 -1
33  -1 -1 -1 -1 -1  1 -1
77  -1 -1  1  1 -1 -1  1
84   1  1 -1 -1  1 -1  1
90   1 -1 -1  1  1 -1  1
123 -1  1 -1  1  1  1  1
10   1 -1 -1  1 -1 -1 -1
16   1  1  1  1 -1 -1 -1
28   1  1 -1  1  1 -1 -1
50   1 -1 -1 -1  1  1 -1
61  -1 -1  1  1  1  1 -1
67  -1  1 -1 -1 -1 -1  1
86   1 -1  1 -1  1 -1  1
100  1  1 -1 -1 -1  1  1
5   -1 -1  1 -1 -1 -1 -1
11  -1  1 -1  1 -1 -1 -1
30   1 -1  1  1  1 -1 -1
44   1  1 -1  1 -1  1 -1
56   1  1  1 -1  1  1 -1
66   1 -1 -1 -1 -1 -1  1
95  -1  1  1  1  1 -1  1
110  1 -1  1  1 -1  1  1
38   1 -1  1 -1 -1  1 -1
51  -1  1 -1 -1  1  1 -1
72   1  1  1 -1 -1 -1  1
76   1  1 -1  1 -1 -1  1
105 -1 -1 -1  1 -1  1  1
111 -1  1  1  1 -1  1  1
117 -1 -1  1 -1  1  1  1
128  1  1  1  1  1  1  1

$rows
 [1]   4  17  23  33  77  84  90 123  10  16  28  50  61  67  86 100   5  11  30
[20]  44  56  66  95 110  38  51  72  76 105 111 117 128

agricolae

agricolae is motivated by agricultural applications although the designs are applicable across a variety of fields.

library(agricolae)

Attaching package: 'agricolae'
The following object is masked from 'package:igraph':

    similarity

The functions to create the design all begin with the word “design.” and the names of the functions are remnant of the name of the experimental design. E.g. design.rcbd generates a Randomised Complete Block Design and design.split generates a Split Plot Design.

ls("package:agricolae") %>% 
  str_subset("^design.")
 [1] "design.ab"      "design.alpha"   "design.bib"     "design.crd"    
 [5] "design.cyclic"  "design.dau"     "design.graeco"  "design.lattice"
 [9] "design.lsd"     "design.mat"     "design.rcbd"    "design.split"  
[13] "design.strip"   "design.youden"

Rather than going through each of the functions, I’ll just show one. The command below generates a balanced incomplete block design with 7 treatments of block size 3. This the same design structure as the first example for AlgDesign. What do you think of the input and output?

trt <- LETTERS[1:7]
design.bib(trt = trt, k = 3)

Parameters BIB
==============
Lambda     : 1
treatmeans : 7
Block size : 3
Blocks     : 7
Replication: 3 

Efficiency factor 0.7777778 

<<< Book >>>
$parameters
$parameters$design
[1] "bib"

$parameters$trt
[1] "A" "B" "C" "D" "E" "F" "G"

$parameters$k
[1] 3

$parameters$serie
[1] 2

$parameters$seed
[1] 1804898417

$parameters$kinds
[1] "Super-Duper"


$statistics
       lambda treatmeans blockSize blocks r Efficiency
values      1          7         3      7 3  0.7777778

$sketch
     [,1] [,2] [,3]
[1,] "C"  "B"  "D" 
[2,] "A"  "E"  "B" 
[3,] "F"  "B"  "G" 
[4,] "G"  "C"  "E" 
[5,] "G"  "A"  "D" 
[6,] "A"  "F"  "C" 
[7,] "F"  "E"  "D" 

$book
   plots block trt
1    101     1   C
2    102     1   B
3    103     1   D
4    201     2   A
5    202     2   E
6    203     2   B
7    301     3   F
8    302     3   B
9    303     3   G
10   401     4   G
11   402     4   C
12   403     4   E
13   501     5   G
14   502     5   A
15   503     5   D
16   601     6   A
17   602     6   F
18   603     6   C
19   701     7   F
20   702     7   E
21   703     7   D

More examples are given in the agricolae tutorial.

lhs

The lhs package is completely different to the previous two packages. It implements methods for creating and augmenting Latin Hypercube Samples and Orthogonal Array Latin Hypercube Samples. The treatment variables here are the parameters and are continuous. In the example below, there are 10 parameters were 30 samples will be drawn from.

library(lhs)
# a design with 30 samples from 10 parameters
A <- randomLHS(30, 10)
A
            [,1]       [,2]       [,3]       [,4]        [,5]       [,6]
 [1,] 0.85115160 0.80153721 0.26562089 0.24240381 0.386617133 0.57523291
 [2,] 0.03162770 0.11851068 0.20750833 0.22137816 0.737580563 0.37572590
 [3,] 0.94326309 0.99286802 0.55167951 0.04431126 0.073908842 0.33729208
 [4,] 0.15341898 0.23664814 0.45088836 0.02736497 0.276594703 0.77521524
 [5,] 0.53987796 0.69129259 0.61068716 0.68112190 0.840092421 0.18545904
 [6,] 0.34338962 0.91067411 0.50772141 0.46340514 0.543650700 0.04848456
 [7,] 0.87984431 0.18530938 0.28391957 0.80767211 0.636091307 0.40499358
 [8,] 0.74093451 0.94142899 0.47633881 0.93482745 0.101815507 0.83195048
 [9,] 0.22679294 0.05950478 0.70384589 0.84840308 0.046119869 0.20549016
[10,] 0.59543890 0.14230001 0.91973016 0.38743743 0.008173053 0.11180544
[11,] 0.71222052 0.84574251 0.05719443 0.33460392 0.414795358 0.71230339
[12,] 0.31313954 0.55023270 0.67189798 0.98743475 0.480147544 0.14900939
[13,] 0.06589897 0.02727366 0.94372045 0.11200430 0.776188787 0.31845634
[14,] 0.67856942 0.64694630 0.11695731 0.57667893 0.576669680 0.68236586
[15,] 0.60779222 0.47346774 0.57803451 0.77359785 0.686925390 0.46043188
[16,] 0.77869112 0.45967726 0.97082607 0.72001527 0.158727598 0.52748006
[17,] 0.47753672 0.33965295 0.34264293 0.88078583 0.932636317 0.08469157
[18,] 0.24829930 0.28054142 0.82863690 0.48987801 0.831406425 0.28007202
[19,] 0.63438918 0.62665931 0.19339855 0.63126047 0.222550404 0.84219677
[20,] 0.42615936 0.78697269 0.31122846 0.54731724 0.618925200 0.98370876
[21,] 0.98558294 0.31283813 0.79937608 0.09708168 0.974254219 0.48614679
[22,] 0.82272308 0.72620385 0.63409490 0.51439160 0.888309555 0.94892286
[23,] 0.28216288 0.40678670 0.00747647 0.15786391 0.462001814 0.89070787
[24,] 0.44293885 0.88759165 0.87593133 0.17614748 0.301809115 0.03273681
[25,] 0.91903885 0.58769320 0.85344414 0.73340894 0.261399107 0.65831637
[26,] 0.39749211 0.21531852 0.40155710 0.40795272 0.175926862 0.54073941
[27,] 0.53326444 0.09494134 0.36906730 0.28462433 0.521423827 0.62613184
[28,] 0.12780125 0.76041647 0.14450865 0.32753635 0.958334555 0.25256769
[29,] 0.19956924 0.39260007 0.76646006 0.65147638 0.353769748 0.90342254
[30,] 0.09115621 0.53145384 0.09544316 0.91317843 0.722981039 0.74109078
            [,7]       [,8]       [,9]      [,10]
 [1,] 0.64829514 0.30957145 0.56063376 0.58060694
 [2,] 0.09386871 0.09460784 0.62699580 0.07496677
 [3,] 0.14971910 0.02306924 0.12609065 0.18310414
 [4,] 0.27273750 0.43275425 0.84548534 0.13991032
 [5,] 0.57024842 0.83876578 0.94430739 0.55675175
 [6,] 0.68468958 0.93462688 0.69388363 0.77296080
 [7,] 0.22736413 0.49914901 0.63951785 0.29475412
 [8,] 0.86262149 0.90864828 0.71549074 0.95154810
 [9,] 0.82450164 0.34137614 0.35590469 0.33383492
[10,] 0.99755568 0.77506400 0.90850387 0.04070513
[11,] 0.51386141 0.51188486 0.74575618 0.47042600
[12,] 0.62716610 0.60853776 0.19349115 0.85808318
[13,] 0.36810057 0.68906398 0.48416759 0.10075997
[14,] 0.46367072 0.53735362 0.97946521 0.53084746
[15,] 0.79151449 0.39841726 0.16295411 0.32738380
[16,] 0.73055037 0.10636268 0.45184454 0.60852297
[17,] 0.11492100 0.64512714 0.26197028 0.87144705
[18,] 0.90350371 0.27696270 0.41905694 0.25261507
[19,] 0.41560144 0.73423244 0.01653787 0.01640204
[20,] 0.54984313 0.26617569 0.32944947 0.20285318
[21,] 0.73515250 0.59964083 0.87721937 0.82147435
[22,] 0.89461948 0.05944528 0.27581653 0.97355201
[23,] 0.95209334 0.17557806 0.57880924 0.65490041
[24,] 0.35714952 0.82135876 0.80705301 0.91792197
[25,] 0.31657015 0.44139011 0.39117389 0.72964052
[26,] 0.03568867 0.88231315 0.53096409 0.45227701
[27,] 0.18195056 0.23326926 0.79716759 0.42737304
[28,] 0.48629095 0.72335715 0.07429013 0.67936824
[29,] 0.03184096 0.15672156 0.06023826 0.73960757
[30,] 0.23509647 0.98392432 0.20423196 0.38968498

lhs provides a number of methods to find the optimal design each with their own criteria.

A1 <- optimumLHS(30, 10, maxSweeps = 4, eps = 0.01)
A2 <- maximinLHS(30, 10, dup = 5)
A3 <- improvedLHS(30, 10, dup = 5)
A4 <- geneticLHS(30, 10, pop = 1000, gen = 8, pMut = 0.1, criterium = "S")
A5 <- geneticLHS(30, 10, pop = 1000, gen = 8, pMut = 0.1, criterium = "Maximin")

ez

This is mainly focussed on the analysis of experimental data but some functions such as ezDesign is useful for viewing the experimental structure.

library(ez)
data(ANT2)
ezPrecis(ANT2)
Data frame dimensions: 5760 rows, 10 columns
             type missing values      min         max
subnum    numeric       0     20        1          20
group      factor       0      2  Control   Treatment
block     numeric       0      6        1           6
trial      factor       0     48        1          48
cue        factor       0      4     None     Spatial
flank      factor       0      3  Neutral Incongruent
location   factor       0      2     down          up
direction  factor       0      2     left       right
rt        numeric     144   5617 179.5972    657.6986
error     numeric     144      3        0           1
ezDesign(data = ANT2,
         x = trial, 
         y = subnum,
         row = block, 
         col = group)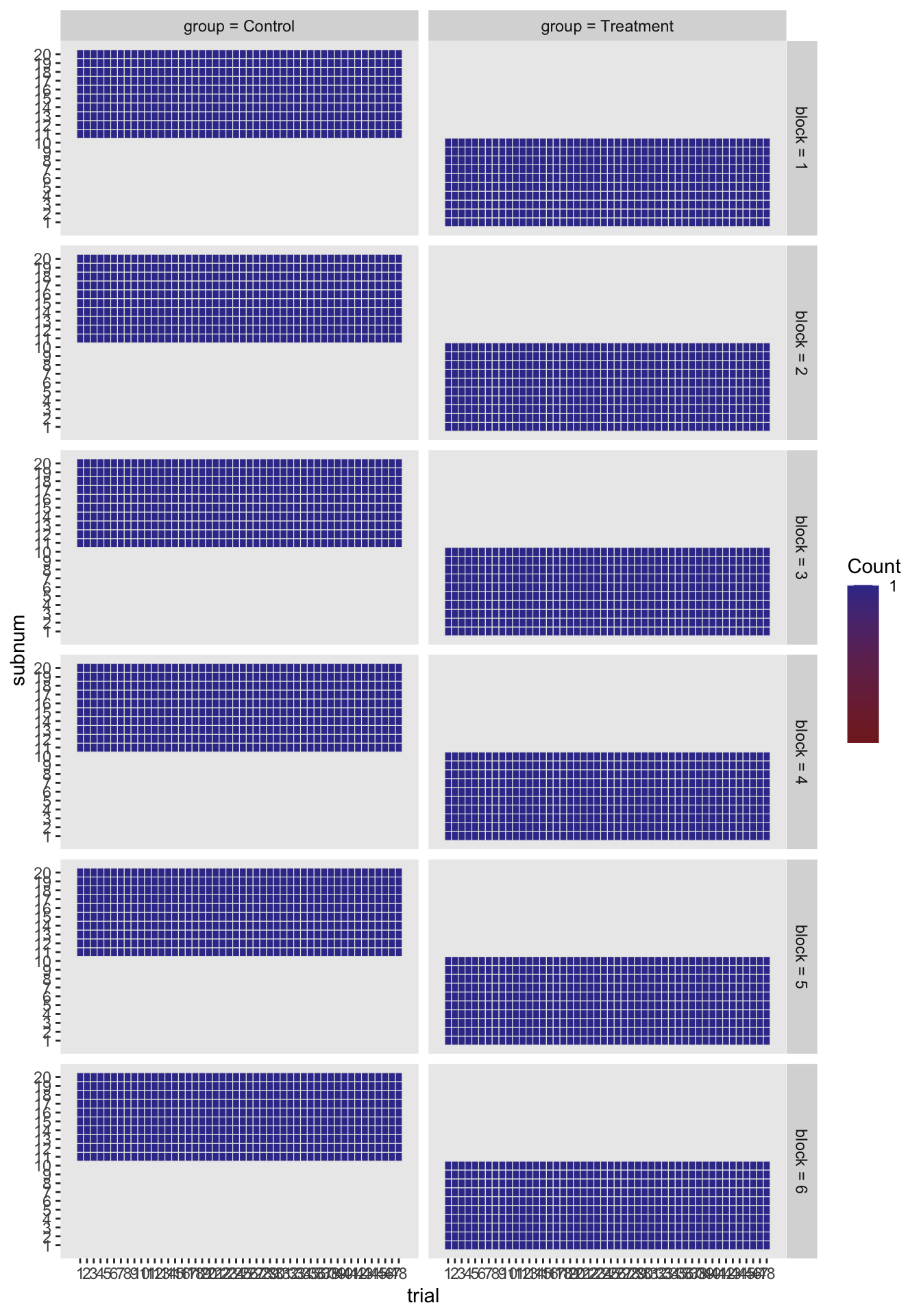

DoE.base

DoE.base provides utility functions for the special class design and as seen in Figure @ref(fig:doe-network), DoE.base is used by four other DoE packages that is maintained also by Prof. Dr. Ulrike Grömping.

DoE.base contains functions to generate factorial designs easily.

library(DoE.base)
Loading required package: grid
Loading required package: conf.design
Registered S3 method overwritten by 'DoE.base':
  method           from       
  factorize.factor conf.design

Attaching package: 'DoE.base'
The following objects are masked from 'package:stats':

    aov, lm
The following object is masked from 'package:graphics':

    plot.design
The following object is masked from 'package:base':

    lengths
fac.design(nlevels = c(2, 2, 3, 3, 6), 
           blocks = 6)
creating full factorial with 216 runs ...
   run.no run.no.std.rp Blocks A B C D E
1       1        29.1.5      1 1 1 2 3 1
2       2       89.1.15      1 1 1 2 2 3
3       3      180.1.30      1 2 2 3 3 5
4       4         4.1.2      1 2 2 1 1 1
5       5       84.1.14      1 2 2 3 1 3
6       6      160.1.28      1 2 2 1 2 5
7       7      118.1.19      1 2 1 3 1 4
8       8      186.1.31      1 2 1 2 1 6
9       9       97.1.17      1 1 1 1 3 3
10     10       92.1.16      1 2 2 2 2 3
11     11      214.1.35      1 2 1 3 3 6
12     12      194.1.33      1 2 1 1 2 6
13     13        39.1.8      1 1 2 1 1 2
14     14         1.1.1      1 1 1 1 1 1
15     15      119.1.20      1 1 2 3 1 4
16     16      127.1.22      1 1 2 2 2 4
17     17      134.1.23      1 2 1 1 3 4
18     18        58.1.9      1 2 1 3 2 2
19     19      135.1.24      1 1 2 1 3 4
20     20      149.1.25      1 1 1 2 1 5
21     21       59.1.10      1 1 2 3 2 2
22     22        38.1.7      1 2 1 1 1 2
23     23       67.1.12      1 1 2 2 3 2
24     24      195.1.34      1 1 2 1 2 6
25     25        32.1.6      1 2 2 2 3 1
26     26       66.1.11      1 2 1 2 3 2
27     27      152.1.26      1 2 2 2 1 5
28     28        21.1.3      1 1 1 3 2 1
29     29      157.1.27      1 1 1 1 2 5
30     30      215.1.36      1 1 2 3 3 6
31     31      100.1.18      1 2 2 1 3 3
32     32      187.1.32      1 1 2 2 1 6
33     33      177.1.29      1 1 1 3 3 5
34     34      126.1.21      1 2 1 2 2 4
35     35       81.1.13      1 1 1 3 1 3
36     36        24.1.4      1 2 2 3 2 1
   run.no run.no.std.rp Blocks A B C D E
37     37        16.2.4      2 2 2 1 2 1
38     38      169.2.29      2 1 1 1 3 5
39     39        43.2.8      2 1 2 2 1 2
40     40      199.2.34      2 1 2 2 2 6
41     41      104.2.18      2 2 2 2 3 3
42     42      206.2.35      2 2 1 1 3 6
43     43      131.2.22      2 1 2 3 2 4
44     44      138.2.23      2 2 1 2 3 4
45     45      172.2.30      2 2 2 1 3 5
46     46      110.2.19      2 2 1 1 1 4
47     47      161.2.27      2 1 1 2 2 5
48     48         5.2.1      2 1 1 2 1 1
49     49        42.2.7      2 2 1 2 1 2
50     50       73.2.13      2 1 1 1 1 3
51     51      191.2.32      2 1 2 3 1 6
52     52       93.2.15      2 1 1 3 2 3
53     53      156.2.26      2 2 2 3 1 5
54     54       96.2.16      2 2 2 3 2 3
55     55       51.2.10      2 1 2 1 2 2
56     56      101.2.17      2 1 1 2 3 3
57     57        13.2.3      2 1 1 1 2 1
58     58      111.2.20      2 1 2 1 1 4
59     59      130.2.21      2 2 1 3 2 4
60     60       76.2.14      2 2 2 1 1 3
61     61      198.2.33      2 2 1 2 2 6
62     62      190.2.31      2 2 1 3 1 6
63     63        33.2.5      2 1 1 3 3 1
64     64      153.2.25      2 1 1 3 1 5
65     65      164.2.28      2 2 2 2 2 5
66     66        50.2.9      2 2 1 1 2 2
67     67      207.2.36      2 1 2 1 3 6
68     68       71.2.12      2 1 2 3 3 2
69     69        36.2.6      2 2 2 3 3 1
70     70         8.2.2      2 2 2 2 1 1
71     71       70.2.11      2 2 1 3 3 2
72     72      139.2.24      2 1 2 2 3 4
    run.no run.no.std.rp Blocks A B C D E
73      73       85.3.15      3 1 1 1 2 3
74      74      105.3.17      3 1 1 3 3 3
75      75        17.3.3      3 1 1 2 2 1
76      76      211.3.36      3 1 2 2 3 6
77      77      114.3.19      3 2 1 2 1 4
78      78        47.3.8      3 1 2 3 1 2
79      79       55.3.10      3 1 2 2 2 2
80      80      182.3.31      3 2 1 1 1 6
81      81      168.3.28      3 2 2 3 2 5
82      82      165.3.27      3 1 1 3 2 5
83      83      142.3.23      3 2 1 3 3 4
84      84      145.3.25      3 1 1 1 1 5
85      85       62.3.11      3 2 1 1 3 2
86      86      148.3.26      3 2 2 1 1 5
87      87      108.3.18      3 2 2 3 3 3
88      88        25.3.5      3 1 1 1 3 1
89      89         9.3.1      3 1 1 3 1 1
90      90       77.3.13      3 1 1 2 1 3
91      91      122.3.21      3 2 1 1 2 4
92      92        12.3.2      3 2 2 3 1 1
93      93        46.3.7      3 2 1 3 1 2
94      94       88.3.16      3 2 2 1 2 3
95      95        20.3.4      3 2 2 2 2 1
96      96        54.3.9      3 2 1 2 2 2
97      97      203.3.34      3 1 2 3 2 6
98      98       80.3.14      3 2 2 2 1 3
99      99      123.3.22      3 1 2 1 2 4
100    100      173.3.29      3 1 1 2 3 5
101    101        28.3.6      3 2 2 1 3 1
102    102      176.3.30      3 2 2 2 3 5
103    103      202.3.33      3 2 1 3 2 6
104    104      115.3.20      3 1 2 2 1 4
105    105      210.3.35      3 2 1 2 3 6
106    106      183.3.32      3 1 2 1 1 6
107    107       63.3.12      3 1 2 1 3 2
108    108      143.3.24      3 1 2 3 3 4
    run.no run.no.std.rp Blocks A B C D E
109    109      179.4.30      4 1 2 3 3 5
110    110      151.4.26      4 1 2 2 1 5
111    111       60.4.10      4 2 2 3 2 2
112    112        31.4.6      4 1 2 2 3 1
113    113         3.4.2      4 1 2 1 1 1
114    114        22.4.3      4 2 1 3 2 1
115    115       99.4.18      4 1 2 1 3 3
116    116        30.4.5      4 2 1 2 3 1
117    117       68.4.12      4 2 2 2 3 2
118    118      196.4.34      4 2 2 1 2 6
119    119       90.4.15      4 2 1 2 2 3
120    120        57.4.9      4 1 1 3 2 2
121    121      158.4.27      4 2 1 1 2 5
122    122      193.4.33      4 1 1 1 2 6
123    123      136.4.24      4 2 2 1 3 4
124    124       82.4.13      4 2 1 3 1 3
125    125       65.4.11      4 1 1 2 3 2
126    126        37.4.7      4 1 1 1 1 2
127    127      120.4.20      4 2 2 3 1 4
128    128      178.4.29      4 2 1 3 3 5
129    129      128.4.22      4 2 2 2 2 4
130    130      188.4.32      4 2 2 2 1 6
131    131         2.4.1      4 2 1 1 1 1
132    132       91.4.16      4 1 2 2 2 3
133    133      185.4.31      4 1 1 2 1 6
134    134      159.4.28      4 1 2 1 2 5
135    135       98.4.17      4 2 1 1 3 3
136    136        40.4.8      4 2 2 1 1 2
137    137      150.4.25      4 2 1 2 1 5
138    138      125.4.21      4 1 1 2 2 4
139    139       83.4.14      4 1 2 3 1 3
140    140      133.4.23      4 1 1 1 3 4
141    141        23.4.4      4 1 2 3 2 1
142    142      117.4.19      4 1 1 3 1 4
143    143      216.4.36      4 2 2 3 3 6
144    144      213.4.35      4 1 1 3 3 6
    run.no run.no.std.rp Blocks A B C D E
145    145      171.5.30      5 1 2 1 3 5
146    146      102.5.17      5 2 1 2 3 3
147    147      162.5.27      5 2 1 2 2 5
148    148      112.5.20      5 2 2 1 1 4
149    149      154.5.25      5 2 1 3 1 5
150    150       74.5.13      5 2 1 1 1 3
151    151      163.5.28      5 1 2 2 2 5
152    152        15.5.4      5 1 2 1 2 1
153    153       72.5.12      5 2 2 3 3 2
154    154       95.5.16      5 1 2 3 2 3
155    155      205.5.35      5 1 1 1 3 6
156    156        35.5.6      5 1 2 3 3 1
157    157         7.5.2      5 1 2 2 1 1
158    158      129.5.21      5 1 1 3 2 4
159    159         6.5.1      5 2 1 2 1 1
160    160       75.5.14      5 1 2 1 1 3
161    161      208.5.36      5 2 2 1 3 6
162    162        14.5.3      5 2 1 1 2 1
163    163       94.5.15      5 2 1 3 2 3
164    164      132.5.22      5 2 2 3 2 4
165    165        34.5.5      5 2 1 3 3 1
166    166       69.5.11      5 1 1 3 3 2
167    167      170.5.29      5 2 1 1 3 5
168    168      137.5.23      5 1 1 2 3 4
169    169       52.5.10      5 2 2 1 2 2
170    170      155.5.26      5 1 2 3 1 5
171    171        49.5.9      5 1 1 1 2 2
172    172      200.5.34      5 2 2 2 2 6
173    173        41.5.7      5 1 1 2 1 2
174    174      192.5.32      5 2 2 3 1 6
175    175        44.5.8      5 2 2 2 1 2
176    176      140.5.24      5 2 2 2 3 4
177    177      197.5.33      5 1 1 2 2 6
178    178      109.5.19      5 1 1 1 1 4
179    179      103.5.18      5 1 2 2 3 3
180    180      189.5.31      5 1 1 3 1 6
    run.no run.no.std.rp Blocks A B C D E
181    181      106.6.17      6 2 1 3 3 3
182    182      146.6.25      6 2 1 1 1 5
183    183       79.6.14      6 1 2 2 1 3
184    184        53.6.9      6 1 1 2 2 2
185    185      209.6.35      6 1 1 2 3 6
186    186       64.6.12      6 2 2 1 3 2
187    187      166.6.27      6 2 1 3 2 5
188    188        19.6.4      6 1 2 2 2 1
189    189      204.6.34      6 2 2 3 2 6
190    190        26.6.5      6 2 1 1 3 1
191    191       78.6.13      6 2 1 2 1 3
192    192       56.6.10      6 2 2 2 2 2
193    193      181.6.31      6 1 1 1 1 6
194    194      174.6.29      6 2 1 2 3 5
195    195       87.6.16      6 1 2 1 2 3
196    196        10.6.1      6 2 1 3 1 1
197    197      212.6.36      6 2 2 2 3 6
198    198      147.6.26      6 1 2 1 1 5
199    199      107.6.18      6 1 2 3 3 3
200    200        48.6.8      6 2 2 3 1 2
201    201      116.6.20      6 2 2 2 1 4
202    202       86.6.15      6 2 1 1 2 3
203    203      184.6.32      6 2 2 1 1 6
204    204        27.6.6      6 1 2 1 3 1
205    205      124.6.22      6 2 2 1 2 4
206    206      141.6.23      6 1 1 3 3 4
207    207      201.6.33      6 1 1 3 2 6
208    208        18.6.3      6 2 1 2 2 1
209    209        45.6.7      6 1 1 3 1 2
210    210      113.6.19      6 1 1 2 1 4
211    211      167.6.28      6 1 2 3 2 5
212    212      121.6.21      6 1 1 1 2 4
213    213      144.6.24      6 2 2 3 3 4
214    214       61.6.11      6 1 1 1 3 2
215    215      175.6.30      6 1 2 2 3 5
216    216        11.6.2      6 1 2 3 1 1
class=design, type= full factorial.blocked 
NOTE: columns run.no and run.no.std.rp  are annotation, 
 not part of the data frame

It also contains functions to create orthogonal array designs.

des <- oa.design(nlevels = c(rep(2, 8), 8))
des
   A B C D E F G H J
1  1 2 1 2 2 1 2 1 6
2  2 1 2 1 2 1 2 1 2
3  2 1 1 2 2 1 1 2 4
4  2 2 1 1 2 2 1 1 3
5  1 1 1 1 2 2 2 2 5
6  1 1 2 2 2 2 1 1 7
7  1 2 1 2 1 2 1 2 2
8  1 1 1 1 1 1 1 1 1
9  1 2 2 1 2 1 1 2 8
10 1 1 2 2 1 1 2 2 3
11 2 1 2 1 1 2 1 2 6
12 2 1 1 2 1 2 2 1 8
13 2 2 2 2 1 1 1 1 5
14 2 2 1 1 1 1 2 2 7
15 1 2 2 1 1 2 2 1 4
16 2 2 2 2 2 2 2 2 1
class=design, type= oa

If you need to further randomise within a specified block, you can do this using rerandomize.design.

rerandomize.design(des, block = "J")
  run.no run.no.std.rp J A B C D E F G H
1      1         4.7.1 7 1 1 2 2 2 2 1 1
2      2        13.7.2 7 2 2 1 1 1 1 2 2
  run.no run.no.std.rp J A B C D E F G H
3      3         7.4.1 4 1 2 2 1 1 2 2 1
4      4        10.4.2 4 2 1 1 2 2 1 1 2
  run.no run.no.std.rp J A B C D E F G H
5      5        12.2.2 2 2 1 2 1 2 1 2 1
6      6         5.2.1 2 1 2 1 2 1 2 1 2
  run.no run.no.std.rp J A B C D E F G H
7      7        11.6.2 6 2 1 2 1 1 2 1 2
8      8         6.6.1 6 1 2 1 2 2 1 2 1
   run.no run.no.std.rp J A B C D E F G H
9       9         9.8.2 8 2 1 1 2 1 2 2 1
10     10         8.8.1 8 1 2 2 1 2 1 1 2
   run.no run.no.std.rp J A B C D E F G H
11     11         3.3.1 3 1 1 2 2 1 1 2 2
12     12        14.3.2 3 2 2 1 1 2 2 1 1
   run.no run.no.std.rp J A B C D E F G H
13     13        16.1.2 1 2 2 2 2 2 2 2 2
14     14         1.1.1 1 1 1 1 1 1 1 1 1
   run.no run.no.std.rp J A B C D E F G H
15     15         2.5.1 5 1 1 1 1 2 2 2 2
16     16        15.5.2 5 2 2 2 2 1 1 1 1
class=design, type= oa.blocked 
NOTE: columns run.no and run.no.std.rp  are annotation, 
 not part of the data frame

So those were the top 5 DoE packages. The API of the packages are quite distinct. The object that it outputs can vary from a matrix to a list. DoE might be a dull area for many but it’s quite important for the downstream analysis. Perhaps if many of us talk more about it, it may help invigorate the area!

References

Carnell, Rob. 2020. Lhs: Latin Hypercube Samples. https://CRAN.R-project.org/package=lhs.
Chatfield, C. 1985. “The Initial Examination of Data.” Journal of the Royal Statistical Society. Series A 148 (3): 214–53.
de Mendiburu, Felipe. 2020. Agricolae: Statistical Procedures for Agricultural Research. https://CRAN.R-project.org/package=agricolae.
Grömping, Ulrike. 2018. “R Package DoE.base for Factorial Experiments.” Journal of Statistical Software 85 (5): 1–41. https://doi.org/10.18637/jss.v085.i05.
Lawrence, Michael A. 2016. Ez: Easy Analysis and Visualization of Factorial Experiments. https://CRAN.R-project.org/package=ez.
Morgan-Wall, Tyler. 2017. Adjustedcranlogs: Remove Automated and Repeated Downloads from ’RStudio’ ’CRAN’ Download Logs. https://CRAN.R-project.org/package=adjustedcranlogs.
Wheeler, Bob. 2019. AlgDesign: Algorithmic Experimental Design. https://CRAN.R-project.org/package=AlgDesign.

Footnotes

  1. At least from my teaching experience, statistics subjects are primary about the analysis and most research grants I’ve seen are about an analytical method. The analytical focus is reflected also in the R packages; there are 1,907 R-packages on CRAN with the word “analysis” in the title as opposed to 287 R-packages with the word “design” in its title.↩︎

  2. Keeping in mind though that your analysis plan may change once you actually have collected data. This is quite common in the analysis of plant breeding trials since some spatial variation only become apparent only after the data collection.↩︎

  3. I originally had a webscrapping error where I didn’t remove duplicate entries so numbers presented at TokyoR and SSA Webinar had the wrong numbers.↩︎

  4. As of 2022-09-18.↩︎