| X | Y | Z |
|---|---|---|
| 4 | 8 | 12 |
| 3 | 6 | 9 |
| 5 | 10 | 15 |
| 2 | 4 | 6 |
| 1 | 2 | 3 |
| 6 | 12 | 18 |
ETC3250/5250
Introduction to Machine Learning
Dimension reduction
Lecturer: Emi Tanaka
Department of Econometrics and Business Statistics
High dimensional data
- In marketing, we may conduct a survey with a large number of questions about customer experience.
- In finance, there may be several ways to assess the credit worthiness of firms or individuals.
- In economics, the development of a country or state can be measured by using multiple measures.
Summarising many variables
- Summarising many variables into a single index can be useful.
- For example,
- In finance, a credit score summarises all the information about the likelihood of bankruptcy for a company.
- In economics, the Human Development Index (HDI) is a summary measure that takes nation’s income, education and health into account.
- In actuary, the Australian Actuaries Climate Index summarises the frequency of extreme weather.
Weighted linear combination
- A convenient way to combine variables is through a linear combination of variables.
- For example, your grade for this unit: \text{Final} = w_1\text{Assign 1} + w_2\text{Assign 2} + w_3\text{Assign 2} + w_4\text{Exam}
- Here w_1, w_2, w_3 and w_4 are called weights.
- In this unit, w_1 = w_2 = 0.1, w_3 = 0.2 and w_4 = 0.6.
- What is a good way to choose weights?
- Do we also need to summarise data into a single variable?
Dimension reduction
- Dimension reduction involves mapping the data into a lower dimensional space.
- The mapping, or projection, involves learning the lower dimensional representation of the data.
- This can help in for example,
- efficiency in computation or memory,
- visualisation,
- noise removal, and
- so on.
- efficiency in computation or memory,
Toy example
Alternatively,
\begin{bmatrix}1 & 2 & 3\end{bmatrix} \times
| t1 |
|---|
| 4 |
| 3 |
| 5 |
| 2 |
| 1 |
| 6 |
Geometrically
Original: 3D space
Projection: 1D space
\mathbb{R}^3 \rightarrow \mathbb{R}
But how do we find this projection?
Matrix transformations
A toy data
# A tibble: 600 × 2
x1 x2
<dbl> <dbl>
1 -2 -2
2 -2 -1.92
3 -2 -1.84
4 -2 -1.76
5 -2 -1.67
6 -2 -1.59
7 -2 -1.51
8 -2 -1.43
9 -2 -1.35
10 -2 -1.27
# ℹ 590 more rows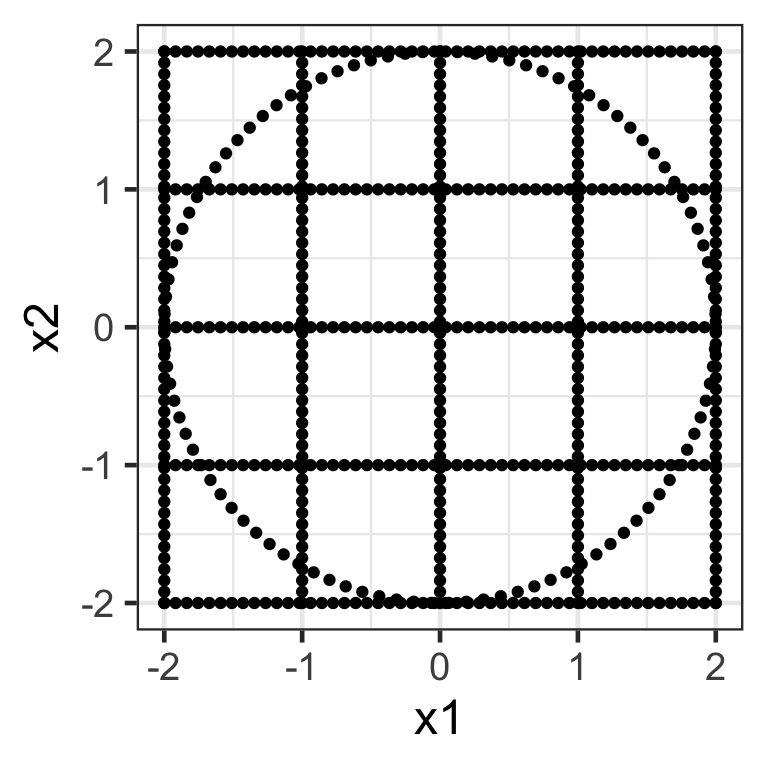
Scaling matrix
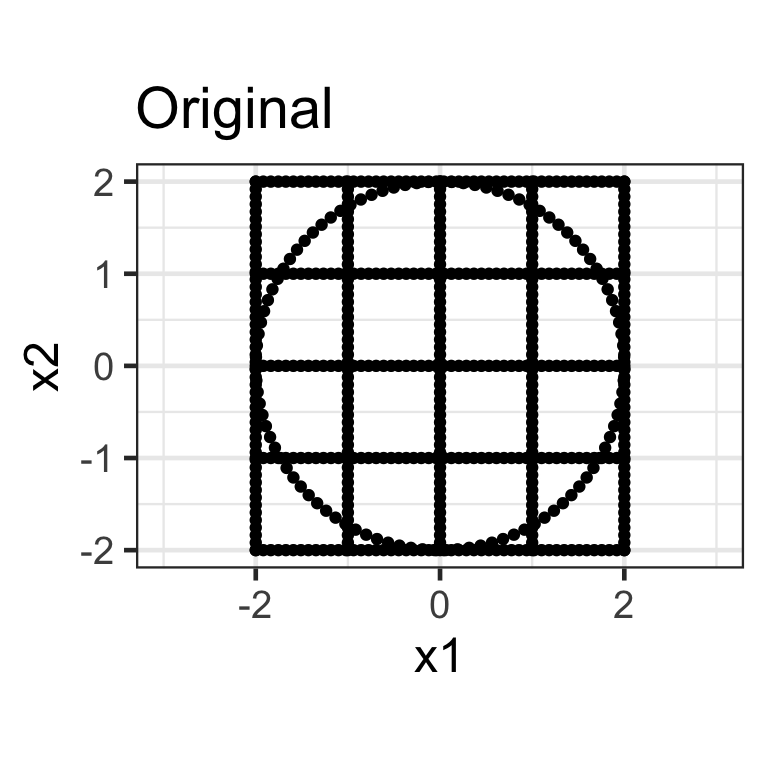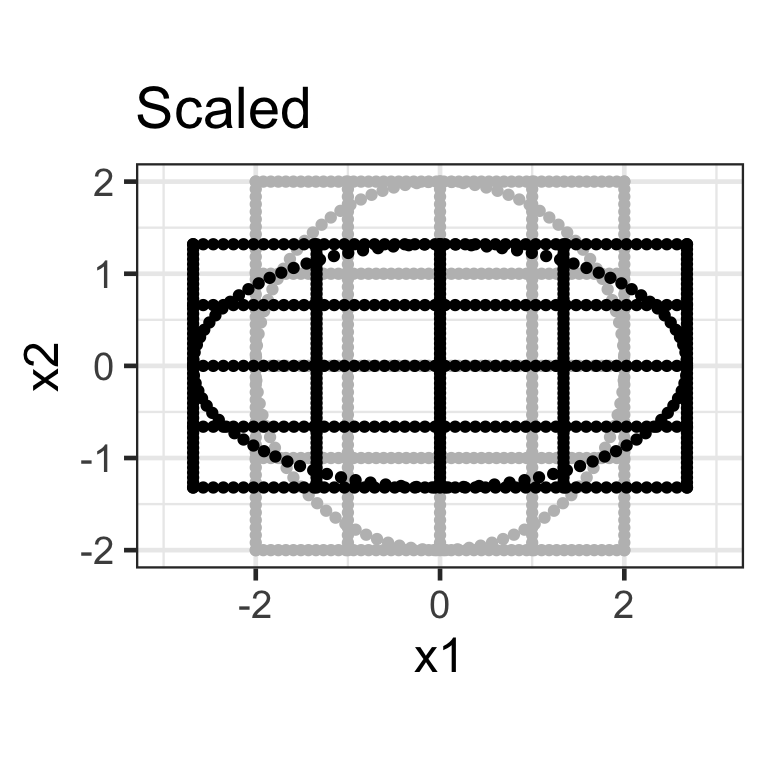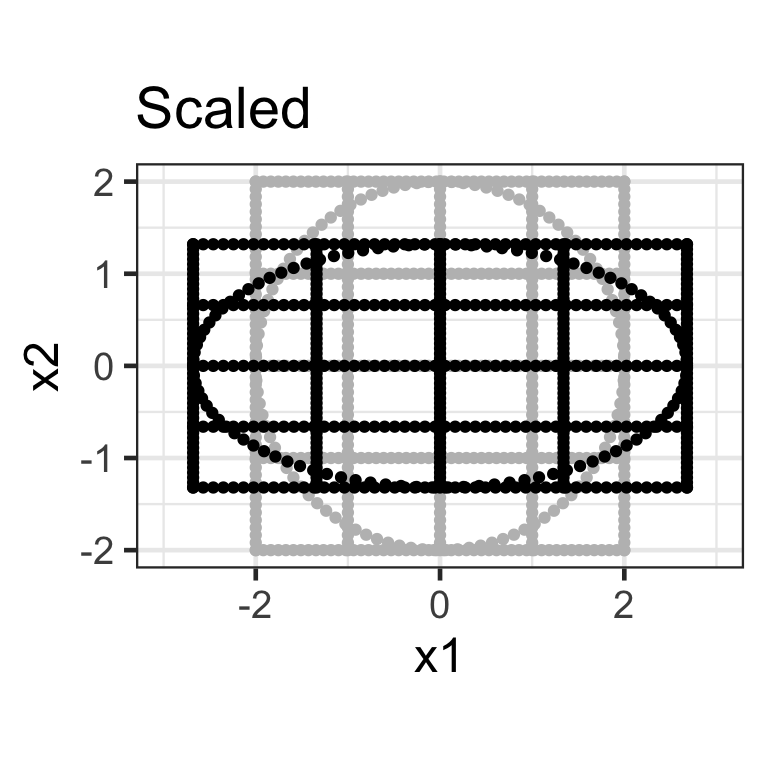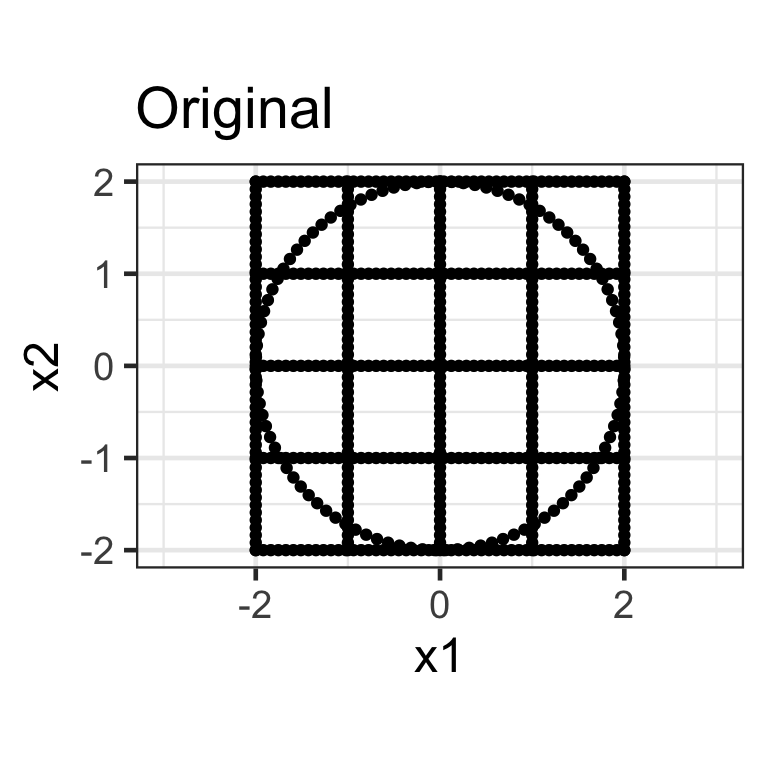
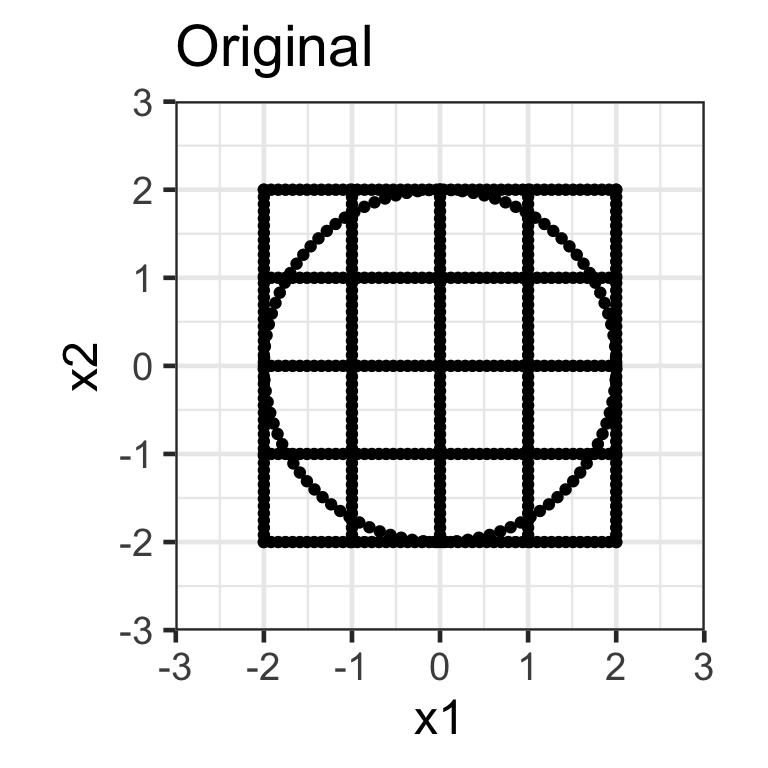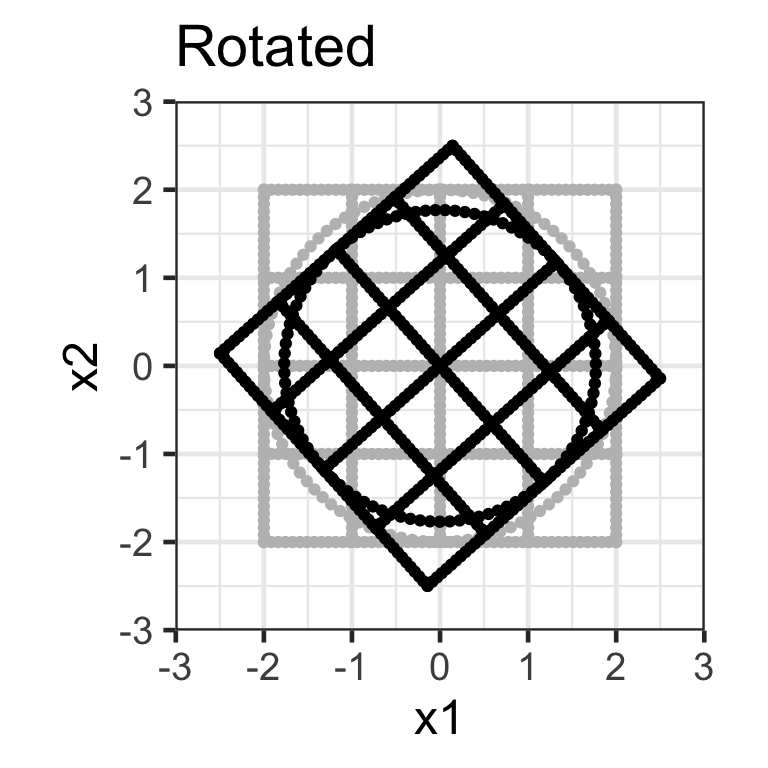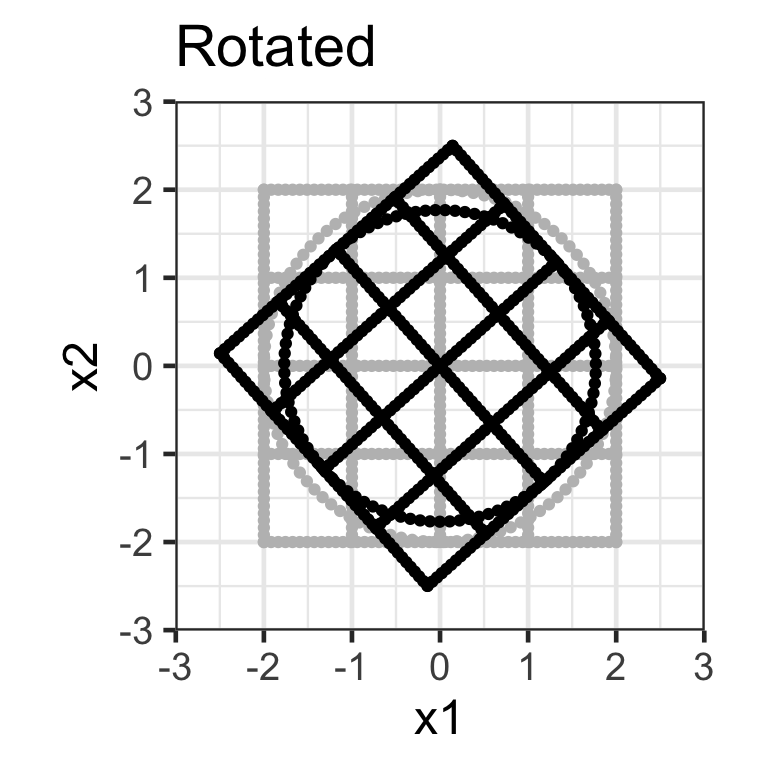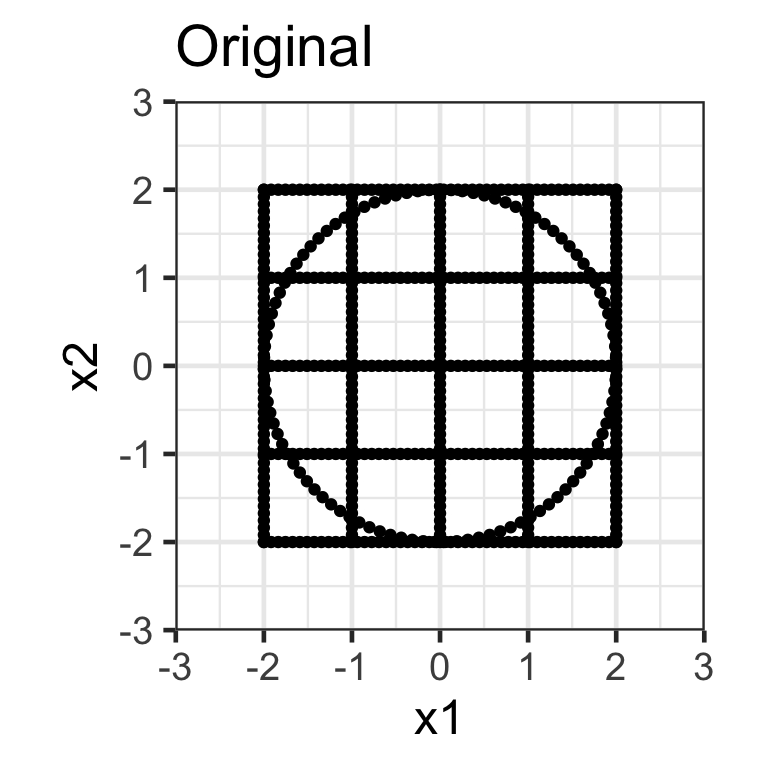
- A diagonal matrix where non-diagonal elements are all zero, e.g. \mathbf{S}_{2\times2} = \begin{bmatrix}s_{x_1} & 0 \\ 0 & s_{x_2}\end{bmatrix}.
- Here we apply the transformation \mathbf{X}_{n\times 2}\mathbf{S}_{2\times2} where \mathbf{S}_{2\times2} = \begin{bmatrix}1.5 & 0 \\ 0 & 0.5\end{bmatrix}.
Rotation matrix
- Applying the transformation \mathbf{X}_{n\times 2}\mathbf{R}_{2\times 2} where \mathbf{R}_{2\times2} = \begin{bmatrix}\cos(\theta) & -\sin(\theta) \\\sin(\theta) & \cos(\theta) \end{bmatrix} rotates the data around the origin by an angle of \theta in the counterclockwise direction.
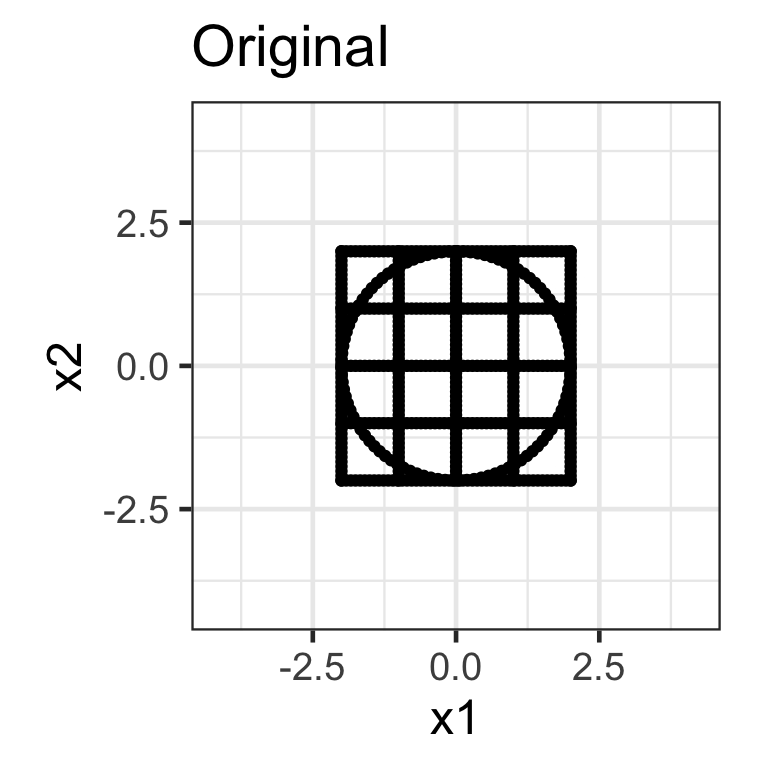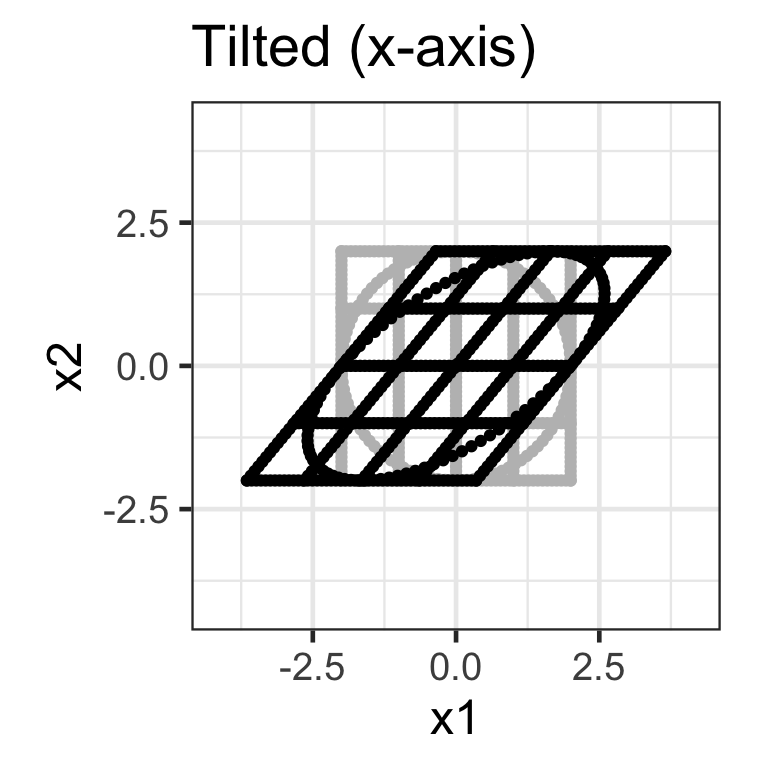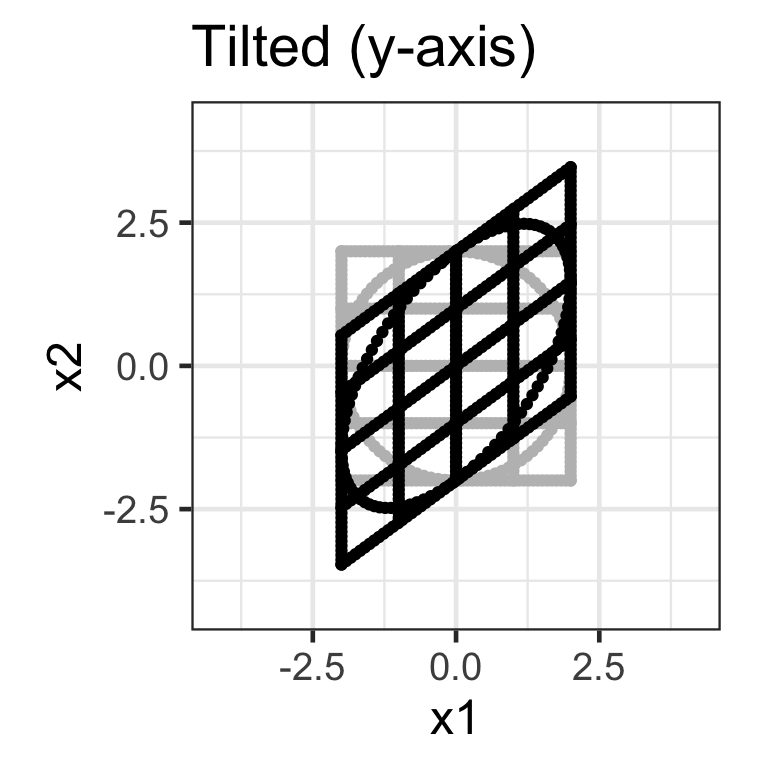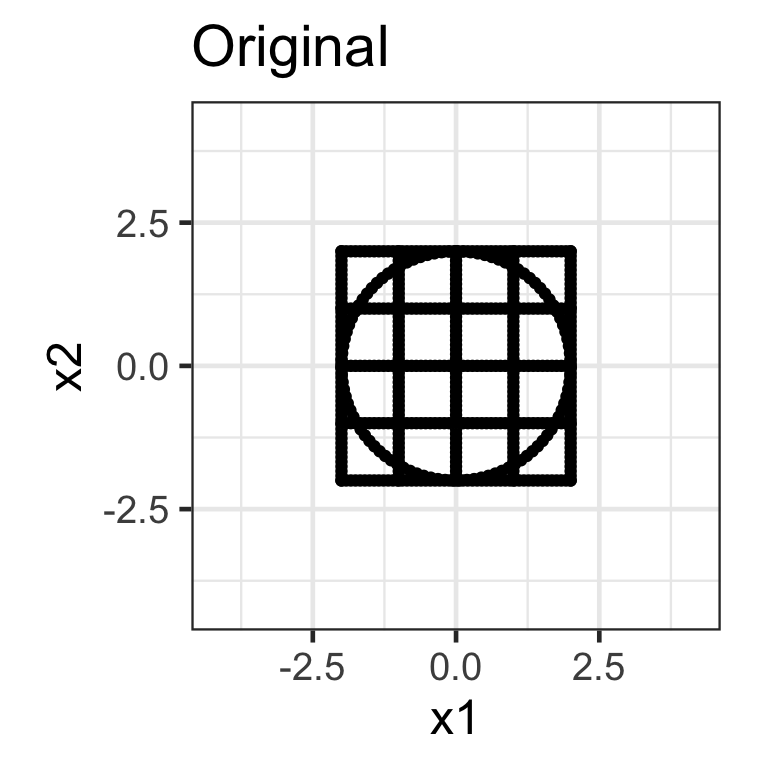
Shear matrix
- A shear matrix can tilt an axis, e.g. \mathbf{H}_{2\times 2} = \begin{bmatrix}1 & \lambda \\ 0 & 1\end{bmatrix} tilts the x-axis.
- The shear matrix below will tilt the y-axis dimension: \mathbf{H}_{2\times 2} = \begin{bmatrix}1 & 0 \\ \lambda & 1\end{bmatrix}.
Inverting transformations
- Suppose we have a new transformed data \hat{\mathbf{X}}_{n\times p} = \mathbf{X}_{n\times p}\mathbf{W}_{p\times p}.
- Then we can get the data in the original measurement by applying: \mathbf{X}_{n\times p} = \hat{\mathbf{X}}_{n\times p}\mathbf{W}^{-1}_{p\times p} provided that \mathbf{W}^{-1} exists.
Matrix decompositions
Eigenvectors and eigenvalues
- For a square matrix, \mathbf{A}, if there exists a vector \boldsymbol{v} and scalar value \lambda such that \mathbf{A}\boldsymbol{v} = \lambda\boldsymbol{v} then \boldsymbol{v} is an eigenvector of \mathbf{A} with eigenvalue of \lambda.
Eigenvalue decomposition
Also called eigendecomposition, diagonalisation or spectral decomposition.
For a positive semi-definite symmetric matrix, \mathbf{V}, there exists an orthogonal matrix \mathbf{Q} and a diagonal matrix \mathbf{\Lambda} such that \mathbf{V} = \mathbf{Q}\mathbf{\Lambda}\mathbf{Q}^{-1}.
\mathbf{\Lambda} is a diagonal matrix where the diagonal entries correspond to eigenvalues.
The columns of \mathbf{Q} are eigenvectors of \mathbf{V} corresponding to the eigenvalues in \mathbf{\Lambda}.
Singular value decomposition
\mathbf{A}_{m\times n} = \mathbf{U}_{m\times m}\mathbf{\Sigma}_{m\times n}\mathbf{V}^\top_{n\times n}
- where
- \mathbf{V} is an orthogonal matrix (i.e. \mathbf{V}^\top\mathbf{V} = \mathbf{I}),
- \mathbf{\Sigma} is a rectangular diagonal matrix, and
- \mathbf{U} is another orthogonal matrix.
- SVD is the same as eigenvalue decomposition if \mathbf{A} is symmetric positive-semidefinite matrix.
Principal components analysis
Principal components
- The k-th principal component is a linear combination of variables: \boldsymbol{t}_k = w_{1k}\boldsymbol{x}_1 + w_{2k}\boldsymbol{x}_2 + \dots + w_{pk}\boldsymbol{x}_p = \mathbf{X}_{n\times p}\boldsymbol{w}_k where \mathbf{X}_{n\times p} = \begin{bmatrix}\boldsymbol{x}_1 & \cdots & \boldsymbol{x}_p \end{bmatrix} and \boldsymbol{w}_k = (w_{1k}, \dots, w_{pk})^\top.
- The elements in \boldsymbol{w}_k are referred to as the loadings (or weights) of the k-th principal component.
- This does assumes all variables are numeric!
Loading or weight matrix
- The matrix \mathbf{W} = \begin{bmatrix}\boldsymbol{w}_1 & \cdots & \boldsymbol{w}_{\min\{n,p\}}\end{bmatrix} is referred to as the loading or weight matrix.
- We obtain the principal component scores (or rotated data) as \mathbf{T} = \begin{bmatrix} \boldsymbol{t}_1 & \cdots & \boldsymbol{t}_{\min\{n,p\}} \end{bmatrix} = \mathbf{X}\mathbf{W}.
First principal components
- The loadings for the first principal component scores are found by maximising the projected variance:
\boldsymbol{w}_1 = \argmax_{\boldsymbol{w}_1} \big\{var(\boldsymbol{t}_1)\big\} = \argmax_{\boldsymbol{w}_1} \big\{var(\mathbf{X}\boldsymbol{w}_1)\big\}.
- Subject to \sum_{j=1}^pw_{j1}^2 = 1.
Second principle component
- The loadings of the second principal component is found from
\boldsymbol{w}_2 = \argmax_{\boldsymbol{w}_2} \big\{var(\boldsymbol{t}_2)\big\} = \argmax_{\boldsymbol{w}_2} \big\{var(\mathbf{X}\boldsymbol{w}_2)\big\}.
- such that \displaystyle\sum_{j=1}^pw_{j2}^2 = 1 and \boldsymbol{w}_1^\top \boldsymbol{w}_2 = 0 (i.e. \boldsymbol{t}_2 is uncorrelated with \boldsymbol{t}_1).
Third principle component and beyond
- The loadings of the third principal component is found from
\boldsymbol{w}_3 = \argmax_{\boldsymbol{w}_3} \big\{var(\boldsymbol{t}_3)\big\} = \argmax_{\boldsymbol{w}_3} \big\{var(\mathbf{X}\boldsymbol{w}_3)\big\}.
- such that \displaystyle\sum_{j=1}^pw_{j3}^2 = 1 and \boldsymbol{t}_3 is uncorrelated with both \boldsymbol{t}_1 and \boldsymbol{t}_2.
- And so on for other higher order PCs.
PCs, eigenvectors and eigenvalues
- Suppose you have a n\times p data matrix \mathbf{X} with each column centered around 0.
- The empirical variance-covariance matrix of the variables is given as \frac{1}{n}\mathbf{X}^\top\mathbf{X}.
- For PCA, we maximise \frac{1}{n}\boldsymbol{w}_k^\top\mathbf{X}^\top\mathbf{X}\boldsymbol{w}_k such that \boldsymbol{w}_k^\top\boldsymbol{w}_k = 1.
- The Lagrangian for this is \frac{1}{n}\boldsymbol{w}_k^\top\mathbf{X}^\top\mathbf{X}\boldsymbol{w}_k-\lambda(\boldsymbol{w}_k^\top\boldsymbol{w}_k - 1).
- The partial derivative with respect to \boldsymbol{w}_k and setting it to zero is 2(\frac{1}{n}\mathbf{X}^\top\mathbf{X} - \lambda\mathbf{I}_n) \boldsymbol{w}_k = 0.
- Therefore, \boldsymbol{w}_k must be an eigenvector of \mathbf{X}^\top\mathbf{X} with eigenvalue of n\lambda.
PCs and SVD
- The PC scores are given as: \mathbf{T} = \mathbf{X}\mathbf{W}.
- Let \mathbf{X} = \mathbf{U}\mathbf{\Sigma}\mathbf{V}^\top.
- It turns out that:
- the columns of \mathbf{U} are the eigenvectors of \mathbf{X}\mathbf{X}^\top,
- the squares of the diagonal elements of \mathbf{\Sigma} are the eigenvalues of both \mathbf{X}^\top\mathbf{X} and \mathbf{X}\mathbf{X}^\top,
- the columns of \mathbf{V} are the eigenvectors of \mathbf{X}^\top\mathbf{X}, and
- \mathbf{W} = \mathbf{V}!
Rotated data
- And so \mathbf{T} = \mathbf{U}\mathbf{\Sigma}\mathbf{W}^\top\mathbf{W} = \mathbf{U}\mathbf{\Sigma}.
- Note that then \mathbf{X} = \mathbf{T}\mathbf{W}^\top.
- You’ll go through more of this in the tutorial.
Geometric interpretation
Alternatively,
- Let \hat{\mathbf{X}}_2 = \mathbf{X} - \mathbf{X}\boldsymbol{w}_1\boldsymbol{w}_1^\top.
- Then \boldsymbol{w}_2 = \argmax_{\boldsymbol{w}_2} \big\{var(\hat{\mathbf{X}}_2\boldsymbol{w}_2)\big\}\text{ such that }\sum_{j=1}^pw_{j2}^2 = 1.
An application to Yale face database
Yale face database
- The data is from P. Belhumeur, J. Hespanha, D. Kriegman, “Eigenfaces vs. Fisherfaces: Recognition Using Class Specific Linear Projection,” IEEE Transactions on Pattern Analysis and Machine Intelligence, July 1997, pp. 711-720.
- The data consists of 15 subjects each under 11 conditions (e.g. “happy”, “sad”, “centerlight”), so a total of 165 images.
- Each image is 320 (width) x 243 (height) = 77,760 pixels (features).
- Note that here n << p!
Sample faces
Code
imagedata_to_plotdata <- function(data = yalefaces,
w = 320,
h = 243,
which = sample(1:165, 15)) {
data %>%
mutate(id = 1:n()) %>%
filter(id %in% which) %>%
pivot_longer(starts_with("V")) %>%
mutate(col = rep(rep(1:w, each = h), n_distinct(id)),
row = rep(rep(1:h, times = w), n_distinct(id)))
}
gfaces <- imagedata_to_plotdata(yalefaces) %>%
ggplot(aes(col, row)) +
geom_tile(aes(fill = value)) +
facet_wrap(~subject + type, nrow = 3) +
scale_y_reverse() +
theme_void(base_size = 18) +
guides(fill = "none") +
coord_equal()
gfaces
Principle component analysis with R
scroll
- There are several functions for doing principal components analysis in R – we use
prcomp().
yalefaces_x <- yalefaces %>%
select(-c(subject, type))
yalefaces_pca <- prcomp(yalefaces_x)
str(yalefaces_pca)List of 5
$ sdev : num [1:165] 10238 6942 5517 5055 4023 ...
$ rotation: num [1:77760, 1:165] -0.000365 -0.000526 -0.000532 -0.000507 -0.00048 ...
..- attr(*, "dimnames")=List of 2
.. ..$ : chr [1:77760] "V1" "V2" "V3" "V4" ...
.. ..$ : chr [1:165] "PC1" "PC2" "PC3" "PC4" ...
$ center : Named num [1:77760] 123 249 250 249 249 ...
..- attr(*, "names")= chr [1:77760] "V1" "V2" "V3" "V4" ...
$ scale : logi FALSE
$ x : num [1:165, 1:165] -7672 -3314 -3065 -16383 -7397 ...
..- attr(*, "dimnames")=List of 2
.. ..$ : NULL
.. ..$ : chr [1:165] "PC1" "PC2" "PC3" "PC4" ...
- attr(*, "class")= chr "prcomp"prcompobject contains:sdevare the standard deviations of the principle componentsrotationis the loading matrixxis the rotated data (centered + scaled data multiplied byrotationmatrix)centeris the centering (if any)scaleis a logical value to indicate if scaling was done
Summary of PCA
- The summary of
prcompobject shows for each PC,- it’s standard deviation,
- the proportion of variation it explains, and
- the cumulative proportion of variation it explains.
- Below shows that PCs of up to (and including) 50 explains 95.11% of the variation in the data.
Importance of components:
PC1 PC2 PC3 PC4 PC5
Standard deviation 1.024e+04 6942.0245 5.517e+03 5.055e+03 4.023e+03
Proportion of Variance 3.054e-01 0.1404 8.869e-02 7.444e-02 4.715e-02
Cumulative Proportion 3.054e-01 0.4458 5.345e-01 6.089e-01 6.561e-01
PC6 PC7 PC8 PC9 PC10
Standard deviation 3.762e+03 3.081e+03 2.812e+03 2.771e+03 2.523e+03
Proportion of Variance 4.123e-02 2.766e-02 2.304e-02 2.237e-02 1.855e-02
Cumulative Proportion 6.973e-01 7.250e-01 7.480e-01 7.704e-01 7.889e-01
PC11 PC12 PC13 PC14 PC15
Standard deviation 2.150e+03 1.998e+03 1.795e+03 1.760e+03 1.731e+03
Proportion of Variance 1.346e-02 1.163e-02 9.390e-03 9.030e-03 8.730e-03
Cumulative Proportion 8.024e-01 8.140e-01 8.234e-01 8.325e-01 8.412e-01
PC16 PC17 PC18 PC19 PC20
Standard deviation 1657.4044 1.586e+03 1.502e+03 1.463e+03 1.432e+03
Proportion of Variance 0.0080 7.320e-03 6.570e-03 6.240e-03 5.970e-03
Cumulative Proportion 0.8492 8.565e-01 8.631e-01 8.693e-01 8.753e-01
PC21 PC22 PC23 PC24 PC25
Standard deviation 1.343e+03 1.291e+03 1.235e+03 1.205e+03 1.147e+03
Proportion of Variance 5.260e-03 4.850e-03 4.450e-03 4.230e-03 3.840e-03
Cumulative Proportion 8.806e-01 8.854e-01 8.899e-01 8.941e-01 8.979e-01
PC26 PC27 PC28 PC29 PC30
Standard deviation 1.144e+03 1.084e+03 1.036e+03 1.018e+03 979.5103
Proportion of Variance 3.810e-03 3.420e-03 3.130e-03 3.020e-03 0.0028
Cumulative Proportion 9.017e-01 9.052e-01 9.083e-01 9.113e-01 0.9141
PC31 PC32 PC33 PC34 PC35
Standard deviation 973.46557 949.70604 926.0579 899.08034 886.35745
Proportion of Variance 0.00276 0.00263 0.0025 0.00236 0.00229
Cumulative Proportion 0.91685 0.91948 0.9220 0.92433 0.92662
PC36 PC37 PC38 PC39 PC40
Standard deviation 854.35433 819.97982 804.40097 797.11137 781.00509
Proportion of Variance 0.00213 0.00196 0.00189 0.00185 0.00178
Cumulative Proportion 0.92874 0.93070 0.93259 0.93444 0.93622
PC41 PC42 PC43 PC44 PC45
Standard deviation 767.79261 753.83380 741.3496 728.30022 717.7012
Proportion of Variance 0.00172 0.00166 0.0016 0.00155 0.0015
Cumulative Proportion 0.93794 0.93959 0.9412 0.94274 0.9442
PC46 PC47 PC48 PC49 PC50
Standard deviation 708.79276 695.40095 681.32271 679.49515 666.06781
Proportion of Variance 0.00146 0.00141 0.00135 0.00135 0.00129
Cumulative Proportion 0.94570 0.94711 0.94846 0.94981 0.95110
PC51 PC52 PC53 PC54 PC55
Standard deviation 659.25153 650.97034 642.5660 634.40640 624.82484
Proportion of Variance 0.00127 0.00123 0.0012 0.00117 0.00114
Cumulative Proportion 0.95237 0.95360 0.9548 0.95598 0.95712
PC56 PC57 PC58 PC59 PC60
Standard deviation 604.43618 602.54879 595.95461 589.03690 584.19071
Proportion of Variance 0.00106 0.00106 0.00103 0.00101 0.00099
Cumulative Proportion 0.95818 0.95924 0.96027 0.96128 0.96228
PC61 PC62 PC63 PC64 PC65
Standard deviation 583.05237 565.14296 558.41544 550.93341 546.82381
Proportion of Variance 0.00099 0.00093 0.00091 0.00088 0.00087
Cumulative Proportion 0.96327 0.96420 0.96511 0.96599 0.96686
PC66 PC67 PC68 PC69 PC70
Standard deviation 538.43362 532.84440 526.71190 524.7713 515.42757
Proportion of Variance 0.00084 0.00083 0.00081 0.0008 0.00077
Cumulative Proportion 0.96771 0.96854 0.96934 0.9701 0.97092
PC71 PC72 PC73 PC74 PC75
Standard deviation 510.56175 508.12438 494.47828 491.91604 489.4362
Proportion of Variance 0.00076 0.00075 0.00071 0.00071 0.0007
Cumulative Proportion 0.97168 0.97243 0.97314 0.97385 0.9746
PC76 PC77 PC78 PC79 PC80
Standard deviation 481.77831 474.38456 470.41992 466.23367 456.39436
Proportion of Variance 0.00068 0.00066 0.00064 0.00063 0.00061
Cumulative Proportion 0.97522 0.97588 0.97652 0.97716 0.97776
PC81 PC82 PC83 PC84 PC85
Standard deviation 454.5586 453.5185 444.90730 441.53940 435.61013
Proportion of Variance 0.0006 0.0006 0.00058 0.00057 0.00055
Cumulative Proportion 0.9784 0.9790 0.97954 0.98011 0.98066
PC86 PC87 PC88 PC89 PC90
Standard deviation 429.57105 426.69337 423.89192 413.2288 411.06527
Proportion of Variance 0.00054 0.00053 0.00052 0.0005 0.00049
Cumulative Proportion 0.98120 0.98173 0.98226 0.9828 0.98324
PC91 PC92 PC93 PC94 PC95
Standard deviation 408.23987 403.71341 400.32073 397.67775 394.87635
Proportion of Variance 0.00049 0.00047 0.00047 0.00046 0.00045
Cumulative Proportion 0.98373 0.98421 0.98467 0.98513 0.98559
PC96 PC97 PC98 PC99 PC100
Standard deviation 390.69468 389.12213 383.96911 382.15048 376.12550
Proportion of Variance 0.00044 0.00044 0.00043 0.00043 0.00041
Cumulative Proportion 0.98603 0.98647 0.98690 0.98733 0.98774
PC101 PC102 PC103 PC104 PC105
Standard deviation 371.2632 365.76624 363.96111 360.61787 355.51007
Proportion of Variance 0.0004 0.00039 0.00039 0.00038 0.00037
Cumulative Proportion 0.9881 0.98853 0.98892 0.98930 0.98967
PC106 PC107 PC108 PC109 PC110
Standard deviation 349.66834 347.69259 344.76632 342.22007 336.67809
Proportion of Variance 0.00036 0.00035 0.00035 0.00034 0.00033
Cumulative Proportion 0.99002 0.99037 0.99072 0.99106 0.99139
PC111 PC112 PC113 PC114 PC115
Standard deviation 333.36005 331.10318 330.25164 326.73677 322.4559
Proportion of Variance 0.00032 0.00032 0.00032 0.00031 0.0003
Cumulative Proportion 0.99172 0.99203 0.99235 0.99266 0.9930
PC116 PC117 PC118 PC119 PC120
Standard deviation 319.0804 317.32550 310.97104 310.16044 306.05539
Proportion of Variance 0.0003 0.00029 0.00028 0.00028 0.00027
Cumulative Proportion 0.9933 0.99356 0.99384 0.99412 0.99439
PC121 PC122 PC123 PC124 PC125
Standard deviation 303.24091 299.56704 297.28634 293.09425 286.00109
Proportion of Variance 0.00027 0.00026 0.00026 0.00025 0.00024
Cumulative Proportion 0.99466 0.99492 0.99518 0.99543 0.99567
PC126 PC127 PC128 PC129 PC130
Standard deviation 282.01505 280.37829 275.73911 271.80841 268.07858
Proportion of Variance 0.00023 0.00023 0.00022 0.00022 0.00021
Cumulative Proportion 0.99590 0.99613 0.99635 0.99656 0.99677
PC131 PC132 PC133 PC134 PC135 PC136
Standard deviation 265.1800 264.0004 259.6532 255.95912 253.99049 250.14523
Proportion of Variance 0.0002 0.0002 0.0002 0.00019 0.00019 0.00018
Cumulative Proportion 0.9970 0.9972 0.9974 0.99757 0.99776 0.99794
PC137 PC138 PC139 PC140 PC141
Standard deviation 243.24003 240.62311 236.08174 232.01663 226.44527
Proportion of Variance 0.00017 0.00017 0.00016 0.00016 0.00015
Cumulative Proportion 0.99811 0.99828 0.99844 0.99860 0.99875
PC142 PC143 PC144 PC145 PC146
Standard deviation 222.92802 2.16e+02 201.99100 199.59454 193.46553
Proportion of Variance 0.00014 1.40e-04 0.00012 0.00012 0.00011
Cumulative Proportion 0.99889 9.99e-01 0.99915 0.99926 0.99937
PC147 PC148 PC149 PC150 PC151
Standard deviation 186.8505 182.9617 179.78968 177.88182 168.71830
Proportion of Variance 0.0001 0.0001 0.00009 0.00009 0.00008
Cumulative Proportion 0.9995 0.9996 0.99967 0.99976 0.99984
PC152 PC153 PC154 PC155 PC156
Standard deviation 139.05249 133.45290 95.80808 87.90070 2.527e-11
Proportion of Variance 0.00006 0.00005 0.00003 0.00002 0.000e+00
Cumulative Proportion 0.99990 0.99995 0.99998 1.00000 1.000e+00
PC157 PC158 PC159 PC160 PC161
Standard deviation 8.795e-12 6.398e-12 5.481e-12 2.854e-12 1.897e-12
Proportion of Variance 0.000e+00 0.000e+00 0.000e+00 0.000e+00 0.000e+00
Cumulative Proportion 1.000e+00 1.000e+00 1.000e+00 1.000e+00 1.000e+00
PC162 PC163 PC164 PC165
Standard deviation 1.095e-12 9.856e-13 7.621e-13 7.621e-13
Proportion of Variance 0.000e+00 0.000e+00 0.000e+00 0.000e+00
Cumulative Proportion 1.000e+00 1.000e+00 1.000e+00 1.000e+00Summary of PCA “by hand”
sdevis simply the sample standard deviation of the rotated data:
PC1 PC2 PC3 PC4 PC5 PC6
10237.892 6942.025 5517.123 5054.695 4022.602 3761.812 [1] 10237.892 6942.025 5517.123 5054.695 4022.602 3761.812- Proportion of variation explained “by hand”:
The total variation of PCs
- There are a total of \min\{p, n\} PCs.
- The total variation of the PCs explain all of the variation of the original variables.
\sum_{j = 1}^{\min\{p,~n\}}var(\boldsymbol{t}_j) = \sum_{j=1}^pvar(\boldsymbol{x}_j)
Image compression

Based on the original data:
165 \times 320 \times 243 \approx 12.8\text{ million}

Based on 50 PCs:
165 \times 50 + 50 \times 320 \times 243 \approx 3.9\text{ million}
Facial recognition
scroll
- Each PC captures a different aspect of the data.
- The PCs can be treated as a feature downstream, say, for facial recognition systems.
















An application to wine quality data
Wine quality data
scroll
This data on wine quality found here.
| Name | wine |
| Number of rows | 6497 |
| Number of columns | 13 |
| _______________________ | |
| Column type frequency: | |
| character | 1 |
| numeric | 12 |
| ________________________ | |
| Group variables | None |
Variable type: character
| skim_variable | n_missing | complete_rate | min | max | empty | n_unique | whitespace |
|---|---|---|---|---|---|---|---|
| type | 0 | 1 | 3 | 5 | 0 | 2 | 0 |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| fixed acidity | 10 | 1 | 7.22 | 1.30 | 3.80 | 6.40 | 7.00 | 7.70 | 15.90 | ▂▇▁▁▁ |
| volatile acidity | 8 | 1 | 0.34 | 0.16 | 0.08 | 0.23 | 0.29 | 0.40 | 1.58 | ▇▂▁▁▁ |
| citric acid | 3 | 1 | 0.32 | 0.15 | 0.00 | 0.25 | 0.31 | 0.39 | 1.66 | ▇▅▁▁▁ |
| residual sugar | 2 | 1 | 5.44 | 4.76 | 0.60 | 1.80 | 3.00 | 8.10 | 65.80 | ▇▁▁▁▁ |
| chlorides | 2 | 1 | 0.06 | 0.04 | 0.01 | 0.04 | 0.05 | 0.06 | 0.61 | ▇▁▁▁▁ |
| free sulfur dioxide | 0 | 1 | 30.53 | 17.75 | 1.00 | 17.00 | 29.00 | 41.00 | 289.00 | ▇▁▁▁▁ |
| total sulfur dioxide | 0 | 1 | 115.74 | 56.52 | 6.00 | 77.00 | 118.00 | 156.00 | 440.00 | ▅▇▂▁▁ |
| density | 0 | 1 | 0.99 | 0.00 | 0.99 | 0.99 | 0.99 | 1.00 | 1.04 | ▇▂▁▁▁ |
| pH | 9 | 1 | 3.22 | 0.16 | 2.72 | 3.11 | 3.21 | 3.32 | 4.01 | ▁▇▆▁▁ |
| sulphates | 4 | 1 | 0.53 | 0.15 | 0.22 | 0.43 | 0.51 | 0.60 | 2.00 | ▇▃▁▁▁ |
| alcohol | 0 | 1 | 10.49 | 1.19 | 8.00 | 9.50 | 10.30 | 11.30 | 14.90 | ▃▇▅▂▁ |
| quality | 0 | 1 | 5.82 | 0.87 | 3.00 | 5.00 | 6.00 | 6.00 | 9.00 | ▁▆▇▃▁ |
- There are small amount missing values in the data.
- For ease of computation, let’s ignore any observations with missing values ( don’t do this in practice!)
Scaling then PCA
wine_pca <- winec %>%
select(-type) %>%
scale() %>%
prcomp() # or skip above line and use prcomp(.scale = TRUE)
wine_pcaStandard deviations (1, .., p=12):
[1] 1.7445303 1.6276285 1.2809541 1.0337025 0.9172812 0.8133844 0.7505644
[8] 0.7178551 0.6768948 0.5460465 0.4767787 0.1808925
Rotation (n x k) = (12 x 12):
PC1 PC2 PC3 PC4
fixed acidity 0.26071445 -0.2589454 0.46564247 -0.14566848
volatile acidity 0.39565721 -0.1017451 -0.28077847 -0.07972791
citric acid -0.14371362 -0.1458295 0.58854048 0.05320974
residual sugar -0.31632548 -0.3455107 -0.07365003 0.11416835
chlorides 0.31574995 -0.2668505 0.04612386 0.16409739
free sulfur dioxide -0.42198110 -0.1158082 -0.09751916 0.30117025
total sulfur dioxide -0.47318123 -0.1486730 -0.10010043 0.13109780
density 0.09751989 -0.5540261 -0.05065537 0.15110768
pH 0.20549880 0.1541321 -0.40589466 0.47551131
sulphates 0.30062120 -0.1172996 0.17132282 0.58618450
alcohol 0.05400002 0.4937868 0.21317892 0.08009431
quality -0.08984644 0.2948571 0.29793560 0.47198353
PC5 PC6 PC7 PC8
fixed acidity 0.164412120 -0.03309162 0.39667040 -0.001027375
volatile acidity 0.147587298 0.37665137 0.44898061 0.308979027
citric acid -0.237540038 -0.36465719 0.04508088 0.442396627
residual sugar 0.507179210 0.06151257 -0.09591307 0.085514113
chlorides -0.391063164 0.42844719 -0.47017478 0.381450232
free sulfur dioxide -0.249063830 0.28146210 0.36627137 0.117939741
total sulfur dioxide -0.224891074 0.10673778 0.23527950 0.011180004
density 0.329530808 -0.15600804 0.01445317 0.041722486
pH -0.005058406 -0.56226140 0.07866747 0.357336224
sulphates -0.195771884 0.02503005 0.16520174 -0.592620308
alcohol 0.113678532 0.16527545 0.33900469 0.229085262
quality 0.460571232 0.27871185 -0.26579816 0.094104102
PC9 PC10 PC11 PC12
fixed acidity -0.4227271729 -0.27139305 -0.276874322 0.3353301943
volatile acidity 0.1286615123 0.49373092 0.141703097 0.0825018577
citric acid 0.2449077627 0.33018866 0.229600749 -0.0009598704
residual sugar 0.4871245444 -0.20979285 0.005346906 0.4508251507
chlorides 0.0376187194 -0.23817399 -0.192321793 0.0429155594
free sulfur dioxide -0.3016225196 -0.30098557 0.487257740 0.0003688274
total sulfur dioxide 0.0003816077 0.29483629 -0.719957849 -0.0638032923
density -0.0709357647 -0.07631692 -0.003674224 -0.7158191738
pH -0.1383458051 -0.11053296 -0.138041136 0.2066358341
sulphates 0.3008084133 0.08242215 0.046234352 0.0777407388
alcohol 0.4159274104 -0.41728072 -0.190397862 -0.3322424355
quality -0.3569784359 0.31037393 -0.017630927 -0.0081246049Standardise or not?
- We can scale in two ways
- Scale the data using
scale() - Include the option
scale. = TRUEwhen callingprcomp()
- Scale the data using
- While the normalisation \sum_{j=1}^{\min\{p,n\}}w_{jk}^2 = 1 is always implemented in any software that does PCA, the decision to standardise is up to you.
- If the variables are measured in the same units then there may be no need to standardise.
- If the variables are measured in the different units then standardise the data.
Proportion of variance by PCs
Importance of components:
PC1 PC2 PC3 PC4 PC5 PC6 PC7
Standard deviation 1.7445 1.6276 1.2810 1.03370 0.91728 0.81338 0.75056
Proportion of Variance 0.2536 0.2208 0.1367 0.08905 0.07012 0.05513 0.04695
Cumulative Proportion 0.2536 0.4744 0.6111 0.70016 0.77028 0.82541 0.87236
PC8 PC9 PC10 PC11 PC12
Standard deviation 0.71786 0.67689 0.54605 0.47678 0.18089
Proportion of Variance 0.04294 0.03818 0.02485 0.01894 0.00273
Cumulative Proportion 0.91530 0.95348 0.97833 0.99727 1.00000Loading matrix
PC1 PC2 PC3 PC4
fixed acidity 0.26071445 -0.2589454 0.46564247 -0.14566848
volatile acidity 0.39565721 -0.1017451 -0.28077847 -0.07972791
citric acid -0.14371362 -0.1458295 0.58854048 0.05320974
residual sugar -0.31632548 -0.3455107 -0.07365003 0.11416835
chlorides 0.31574995 -0.2668505 0.04612386 0.16409739
free sulfur dioxide -0.42198110 -0.1158082 -0.09751916 0.30117025
total sulfur dioxide -0.47318123 -0.1486730 -0.10010043 0.13109780
density 0.09751989 -0.5540261 -0.05065537 0.15110768
pH 0.20549880 0.1541321 -0.40589466 0.47551131
sulphates 0.30062120 -0.1172996 0.17132282 0.58618450
alcohol 0.05400002 0.4937868 0.21317892 0.08009431
quality -0.08984644 0.2948571 0.29793560 0.47198353
PC5 PC6 PC7 PC8
fixed acidity 0.164412120 -0.03309162 0.39667040 -0.001027375
volatile acidity 0.147587298 0.37665137 0.44898061 0.308979027
citric acid -0.237540038 -0.36465719 0.04508088 0.442396627
residual sugar 0.507179210 0.06151257 -0.09591307 0.085514113
chlorides -0.391063164 0.42844719 -0.47017478 0.381450232
free sulfur dioxide -0.249063830 0.28146210 0.36627137 0.117939741
total sulfur dioxide -0.224891074 0.10673778 0.23527950 0.011180004
density 0.329530808 -0.15600804 0.01445317 0.041722486
pH -0.005058406 -0.56226140 0.07866747 0.357336224
sulphates -0.195771884 0.02503005 0.16520174 -0.592620308
alcohol 0.113678532 0.16527545 0.33900469 0.229085262
quality 0.460571232 0.27871185 -0.26579816 0.094104102
PC9 PC10 PC11 PC12
fixed acidity -0.4227271729 -0.27139305 -0.276874322 0.3353301943
volatile acidity 0.1286615123 0.49373092 0.141703097 0.0825018577
citric acid 0.2449077627 0.33018866 0.229600749 -0.0009598704
residual sugar 0.4871245444 -0.20979285 0.005346906 0.4508251507
chlorides 0.0376187194 -0.23817399 -0.192321793 0.0429155594
free sulfur dioxide -0.3016225196 -0.30098557 0.487257740 0.0003688274
total sulfur dioxide 0.0003816077 0.29483629 -0.719957849 -0.0638032923
density -0.0709357647 -0.07631692 -0.003674224 -0.7158191738
pH -0.1383458051 -0.11053296 -0.138041136 0.2066358341
sulphates 0.3008084133 0.08242215 0.046234352 0.0777407388
alcohol 0.4159274104 -0.41728072 -0.190397862 -0.3322424355
quality -0.3569784359 0.31037393 -0.017630927 -0.0081246049- A positive (negative) loading indicates a positive (negative) association between a variable and the corresponding PC.
- The magnitude indicates the strength of the association.
Augment PCs to data
# A tibble: 6 × 26
.rownames type `fixed acidity` `volatile acidity` `citric acid`
<chr> <chr> <dbl> <dbl> <dbl>
1 1 white 7 0.27 0.36
2 2 white 6.3 0.3 0.34
3 3 white 8.1 0.28 0.4
4 4 white 7.2 0.23 0.32
5 5 white 7.2 0.23 0.32
6 6 white 8.1 0.28 0.4
# ℹ 21 more variables: `residual sugar` <dbl>, chlorides <dbl>,
# `free sulfur dioxide` <dbl>, `total sulfur dioxide` <dbl>, density <dbl>,
# pH <dbl>, sulphates <dbl>, alcohol <dbl>, quality <dbl>, .fittedPC1 <dbl>,
# .fittedPC2 <dbl>, .fittedPC3 <dbl>, .fittedPC4 <dbl>, .fittedPC5 <dbl>,
# .fittedPC6 <dbl>, .fittedPC7 <dbl>, .fittedPC8 <dbl>, .fittedPC9 <dbl>,
# .fittedPC10 <dbl>, .fittedPC11 <dbl>, .fittedPC12 <dbl>Visualisations
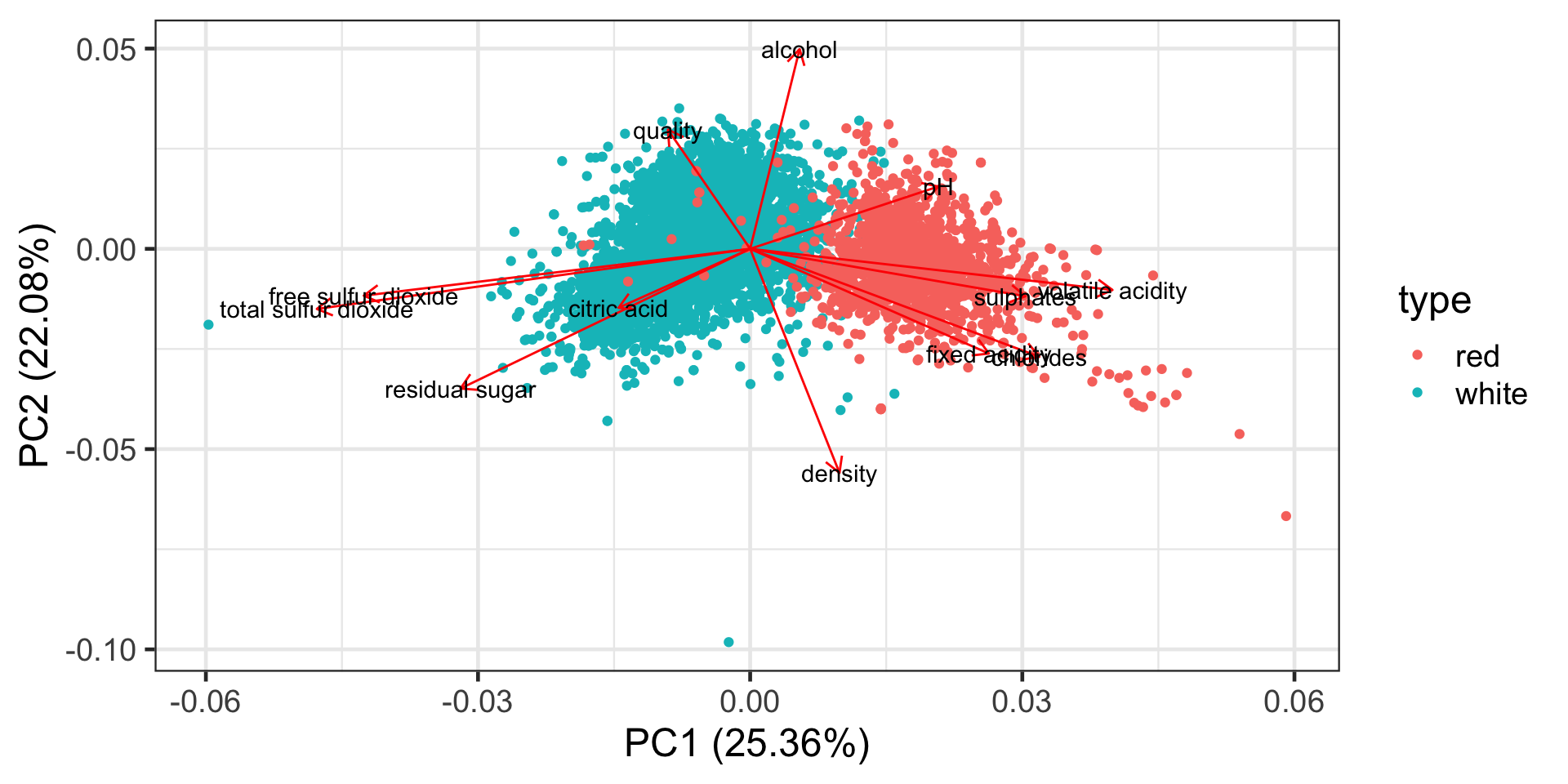
Correlation biplot
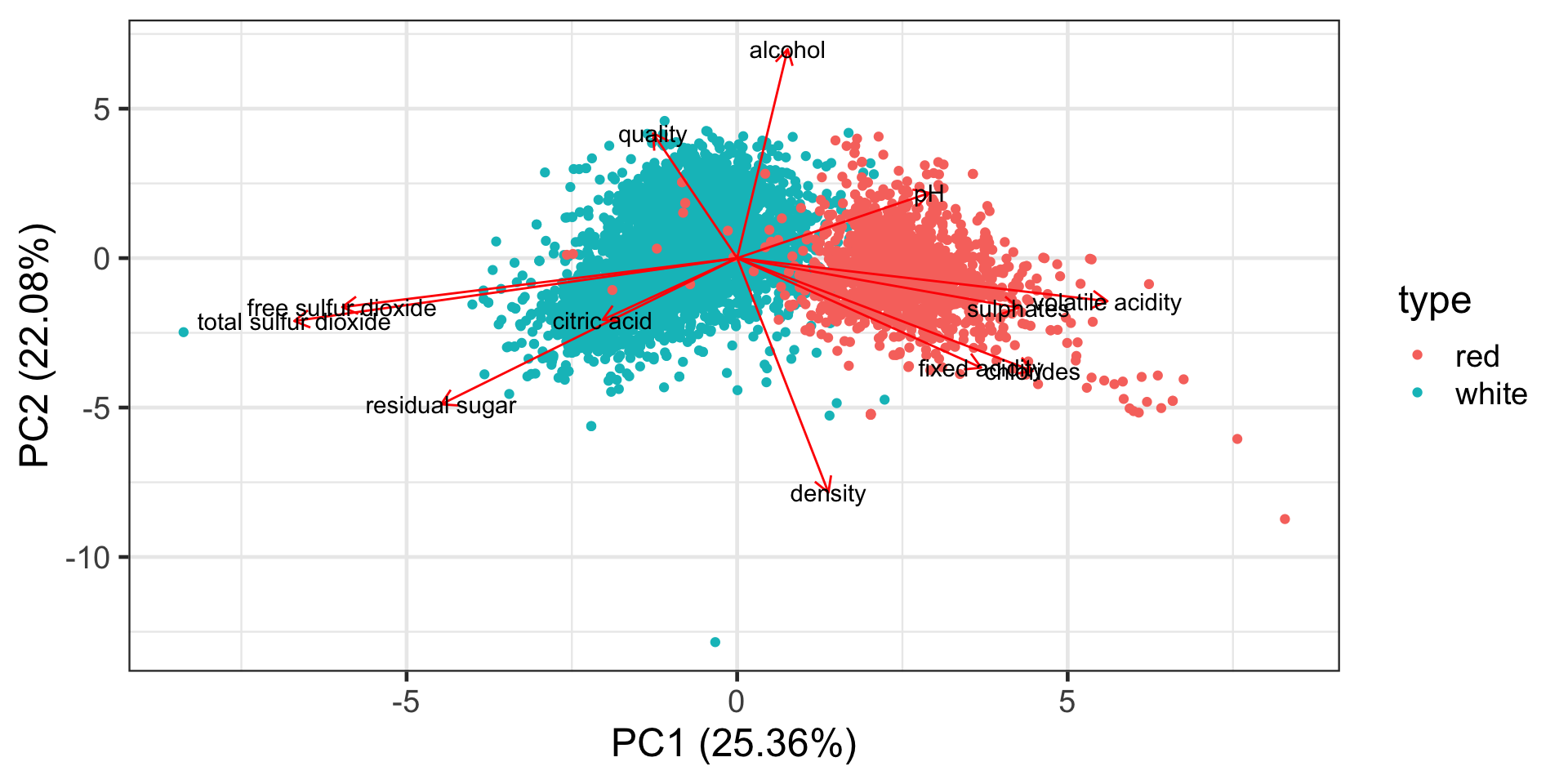
Distance biplot
Interpreting a biplot
- The distance between observations implies similarity between observations.
- The angles between variables tell us something about correlation (approximately)
- citric acid and residual sugar are highly positively correlated as the angle between them is close to zero.
- quality and pH are close to uncorrelated as the angle between them is close 90 degrees.
- pH and citric acid are highly negatively correlated as the angle between them is close to 180 degrees.
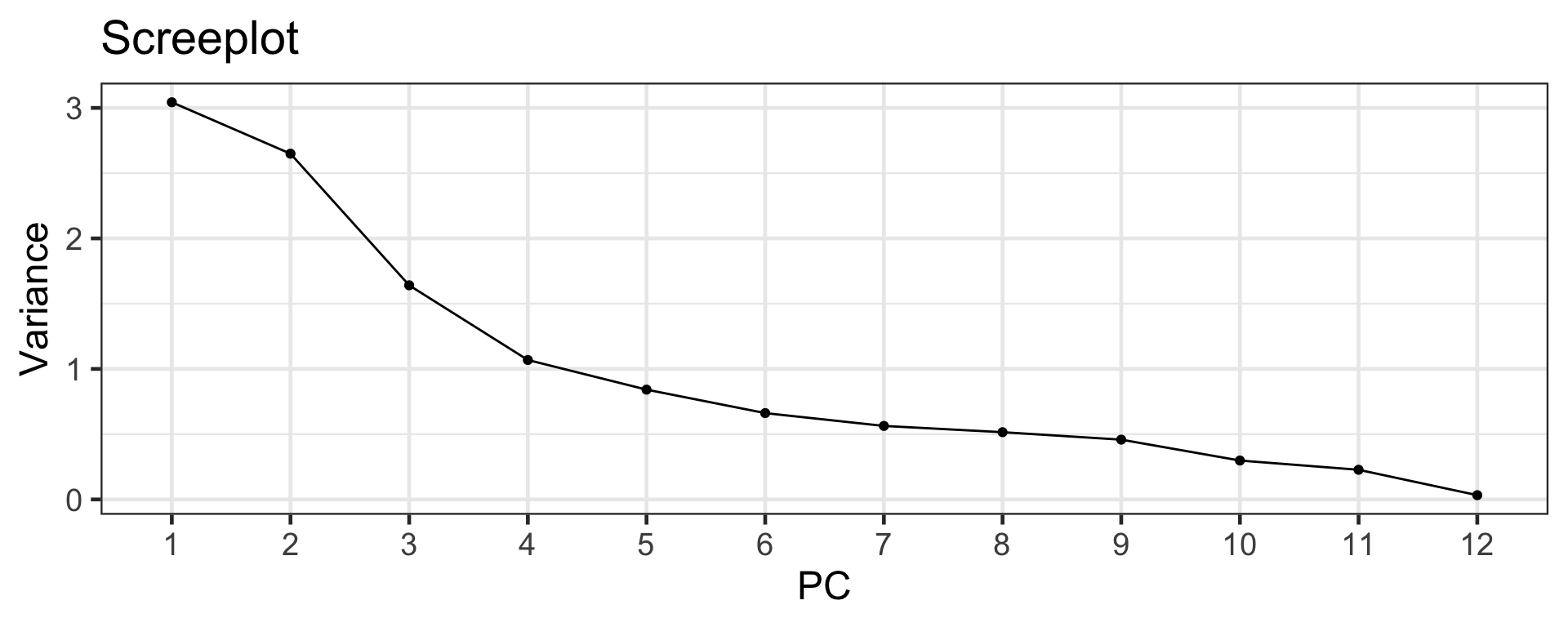
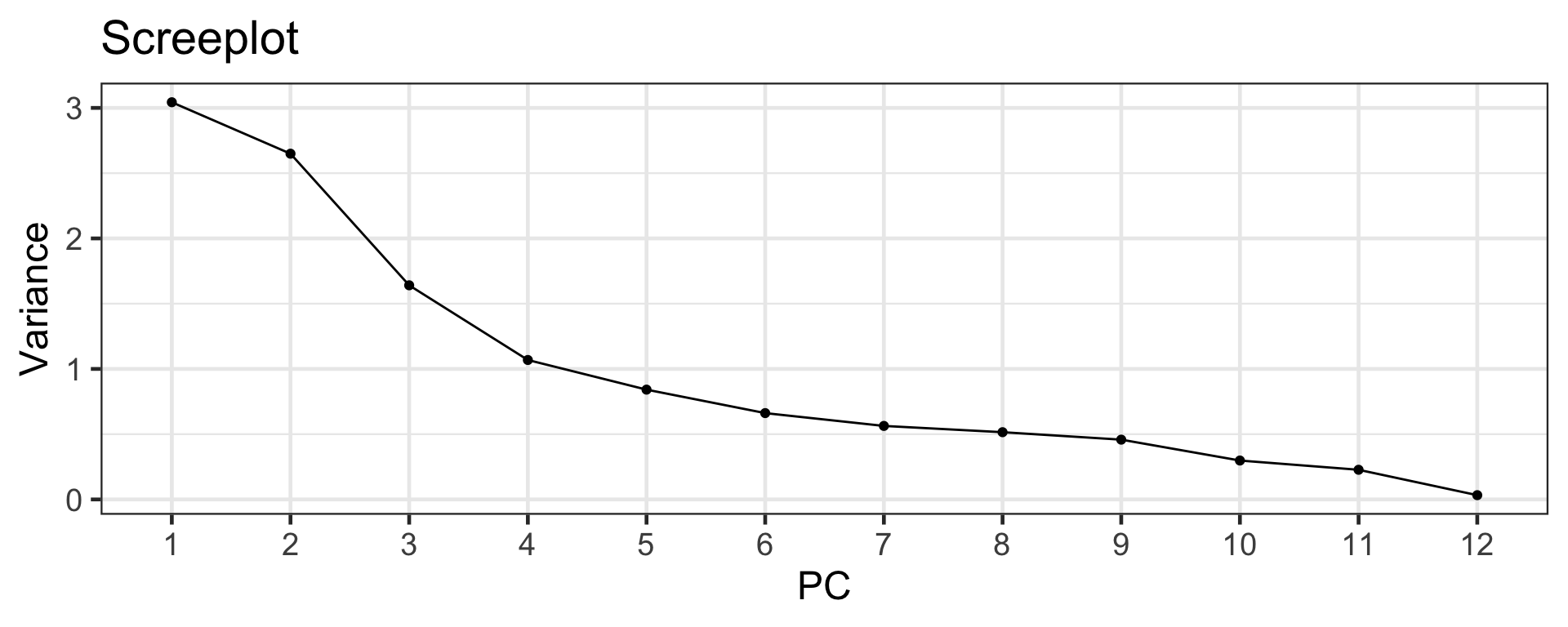
Scree plot
Selecting the number of principal components
Elbow method
- The scree plot can be used to select the number of PCs.
- Look for the “elbow” of the scree plot (around 4-6).
- There is some subjectiveness to the selection!
Kaiser’s rule
- Kaiser’s rule states to select all PCs with a variance greater than 1.
Importance of components:
PC1 PC2 PC3 PC4 PC5 PC6 PC7
Standard deviation 1.7445 1.6276 1.2810 1.03370 0.91728 0.81338 0.75056
Proportion of Variance 0.2536 0.2208 0.1367 0.08905 0.07012 0.05513 0.04695
Cumulative Proportion 0.2536 0.4744 0.6111 0.70016 0.77028 0.82541 0.87236
PC8 PC9 PC10 PC11 PC12
Standard deviation 0.71786 0.67689 0.54605 0.47678 0.18089
Proportion of Variance 0.04294 0.03818 0.02485 0.01894 0.00273
Cumulative Proportion 0.91530 0.95348 0.97833 0.99727 1.00000- Here we select 4 PCs.
Interpreting PCs
- Remember that PCs do nothing more than finding uncorrelated linear combinations of the variables that explain the variance of the data.
- It can be incredibly useful to find the interpretation of PCs but this relies on the context of data.
Multi-dimensional scaling
Motivation
- Suppose we have n observations and p (numerical) variables.
- When p = 2, we can easily draw a scatterplot to see the disances between observations.
- However, when p > 2 then there isn’t an easy way to visualise the distances between observations.
- But, we can get a close approximation of the distances using multi-dimensional scaling (MDS) by finding a low (usually two) dimensional represenation of pairwise distances between observations.
Classical MDS
Dwinec <- winec %>%
# note that we are removing the categorical variable `type` here!
select(-type) %>%
# then standardising the data
scale() %>%
# and calculating the distances between observations (ED is default)
dist()
# add the row labels back
attributes(Dwinec)$Labels <- winec$type
# perform the classical (metric) MDS
mdsout <- cmdscale(Dwinec, k = 2)
head(mdsout) [,1] [,2]
white 2.49817594 3.1644222
white -0.08269114 -0.4738874
white 0.18302503 0.2916830
white 1.75126084 0.7336440
white 1.75126084 0.7336440
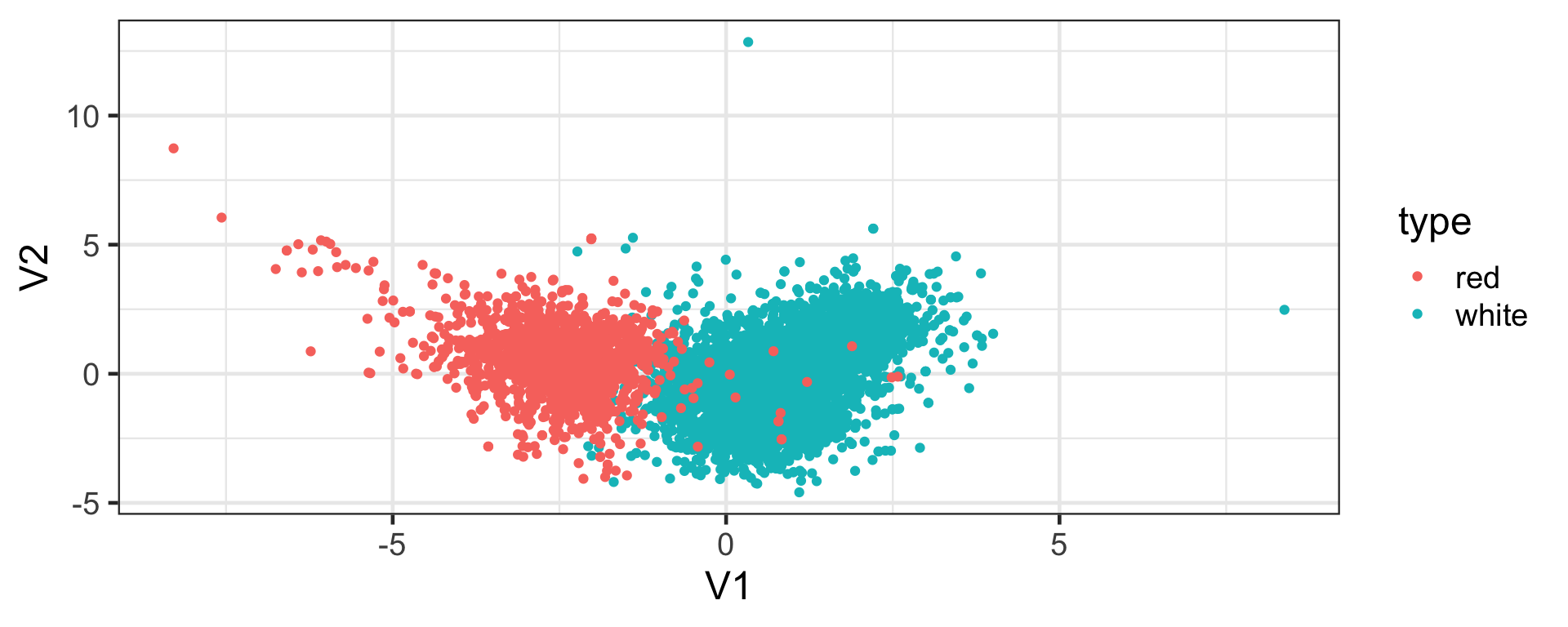
white 0.18302503 0.2916830Visualising the MDS output
Distances
D_{Euclidean}(\boldsymbol{x}_i, \boldsymbol{x}_j) = \sqrt{\sum_{s = 1}^p (x_{is} - x_{js})^2}.
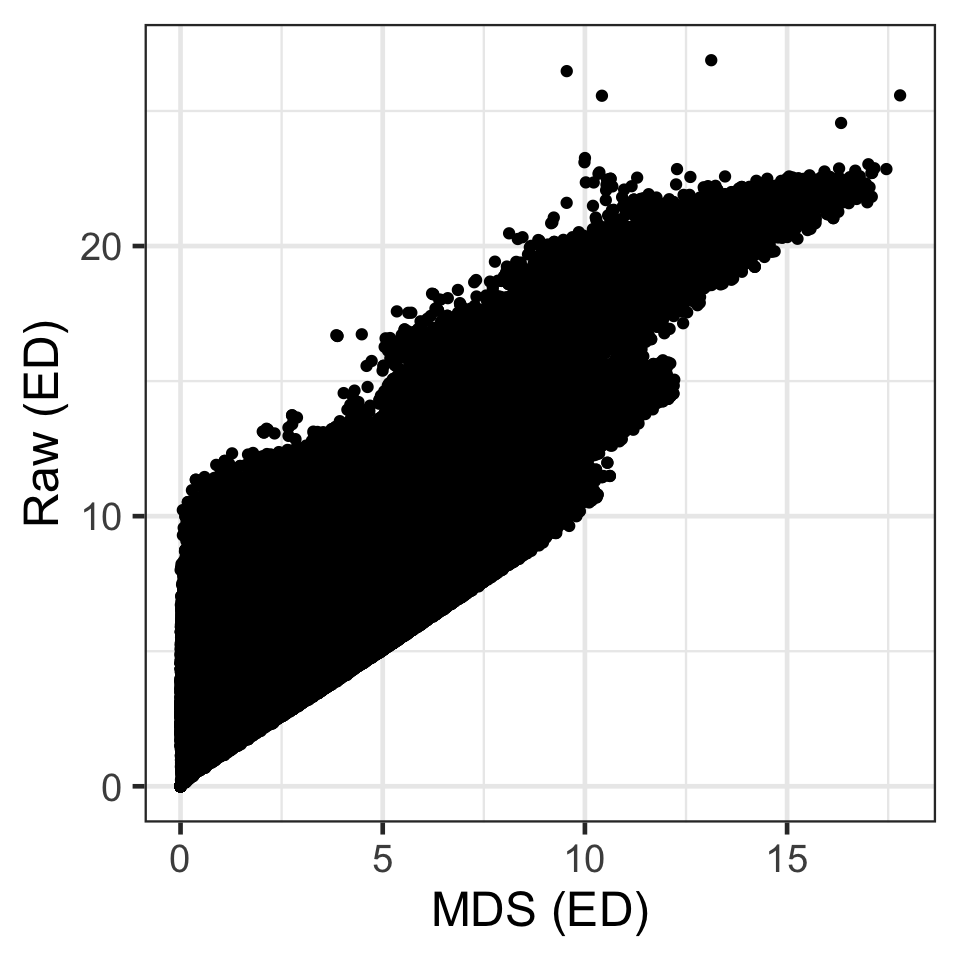
- So for example, D_{Euclidean}(\boldsymbol{x}_1, \boldsymbol{x}_2) = 5.415.
- But for D_{Euclidean}(\boldsymbol{z}_1, \boldsymbol{z}_2) = \sqrt{(2.498 - (-0.083))^2 + (3.164 - (-0.474))^2} = 4.461.
- Another example, D_{Euclidean}(\boldsymbol{x}_1, \boldsymbol{x}_3) = 4.392.
- But D_{Euclidean}(\boldsymbol{z}_1, \boldsymbol{z}_2) = \sqrt{(2.498 - 0.183)^2 + (3.164 - 0.292)^2} = 3.69.
Comparing raw and MDS distances
Classical MDS
- In classical MDS, the aim is to minimise the strain function:
\text{Strain} = \sum_{i=1}^{n-1}\sum_{j>i}\left(D(\boldsymbol{x}_i, \boldsymbol{x}_j) - D(\boldsymbol{z}_i, \boldsymbol{z}_j)\right)^2.
- The above has a tractable solution when Euclidean distance is used.
- The solution rotates the points until the 2D projection is close to the input distances.
Sammon mapping
- An alternative objective is to minimise the stress function:
\text{Stress} = \sum_{i=1}^{n-1}\sum_{j>i}\frac{\left(D(\boldsymbol{x}_i, \boldsymbol{x}_j) - D(\boldsymbol{z}_i, \boldsymbol{z}_j)\right)^2}{D(\boldsymbol{x}_i, \boldsymbol{x}_j)}.
- This ensures that points that observations with small distances are close to in the MDS output as well, preserving the local structure.
- This is refererd to as sammon mapping.
Modern MDS
- Methods for finding a low dimensional representation of high dimensional data are more recently referred to as manifold learning.
- Low-dimensional representations can also be used as features downstream in classification or regression problems.
- Some of these examples include,
- Local linear embeddings (LLE)
- IsoMap
- t-SNE
- UMAP, and so on.
Takeaways
- Principal components are linear combination of the data variables.
- Multi-dimensional scaling is a non-linear dimensionality reduction.
- They both present low-dimenstional representation of the full data and useful for downstream analysis.

ETC3250/5250 Week 8