Code
Introduction to Machine Learning
Lecturer: Emi Tanaka
Department of Econometrics and Business Statistics
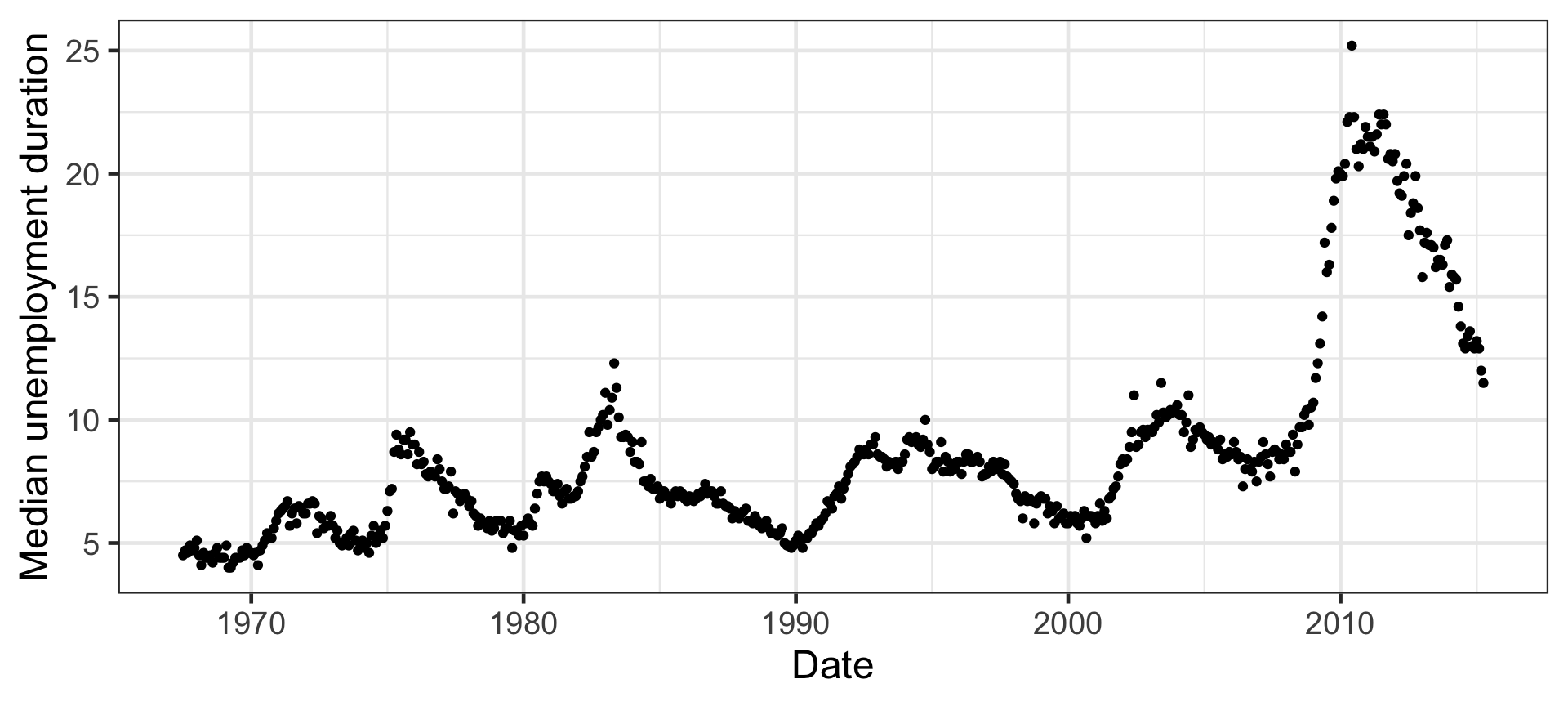
This dataset is available from http://research.stlouisfed.org/fred2.
\color{#006DAE}{y_i = \beta_0 + \beta_1x_{i1}+ \beta_2x_{i1}^2 + \cdots + \beta_{27}x_{i1}^{27} + e_i}
The model can be fitted using the loess function where
In ggplot, you can add the loess using geom_smooth with method = loess and method arguments passed as list:
span changes the loess fit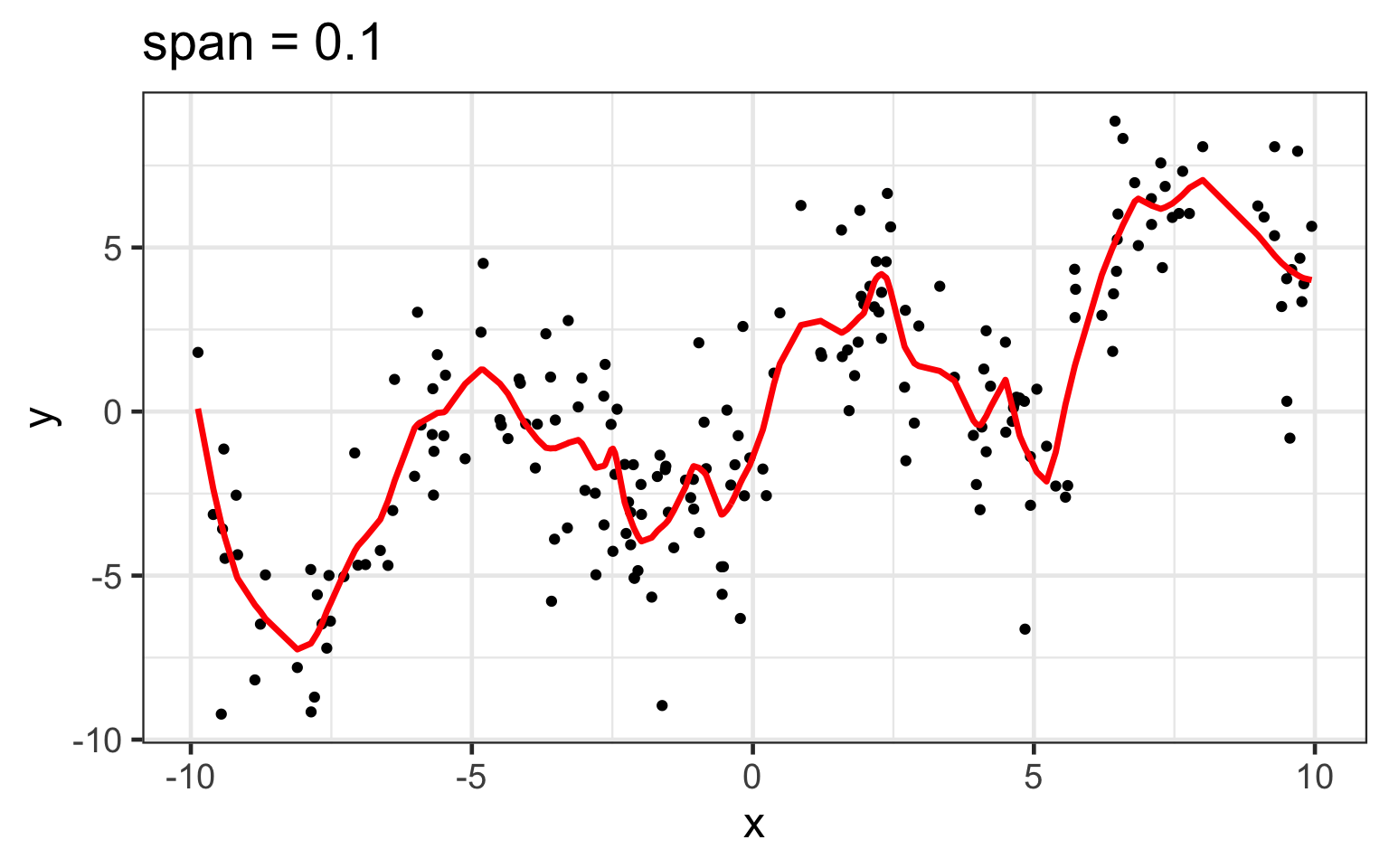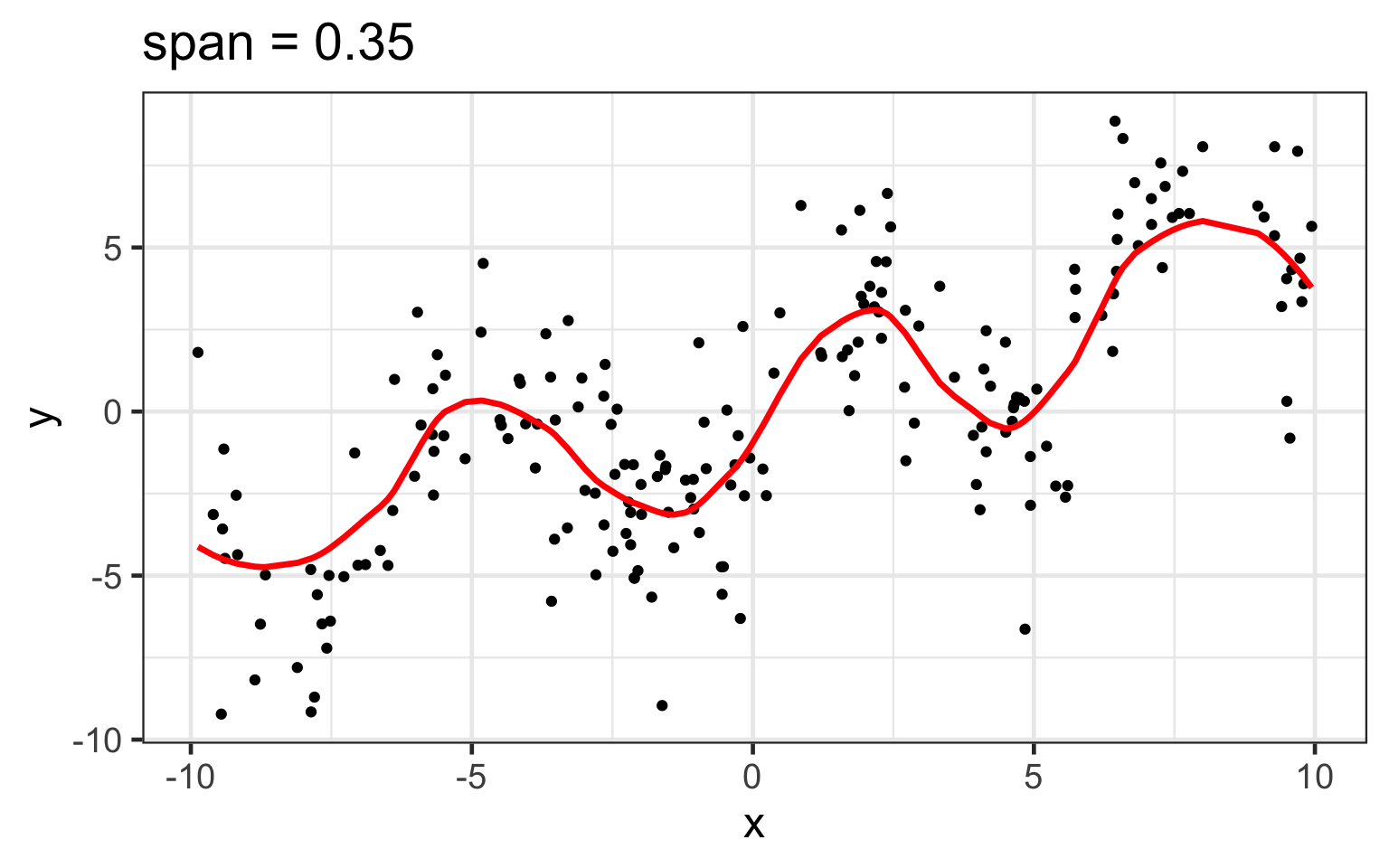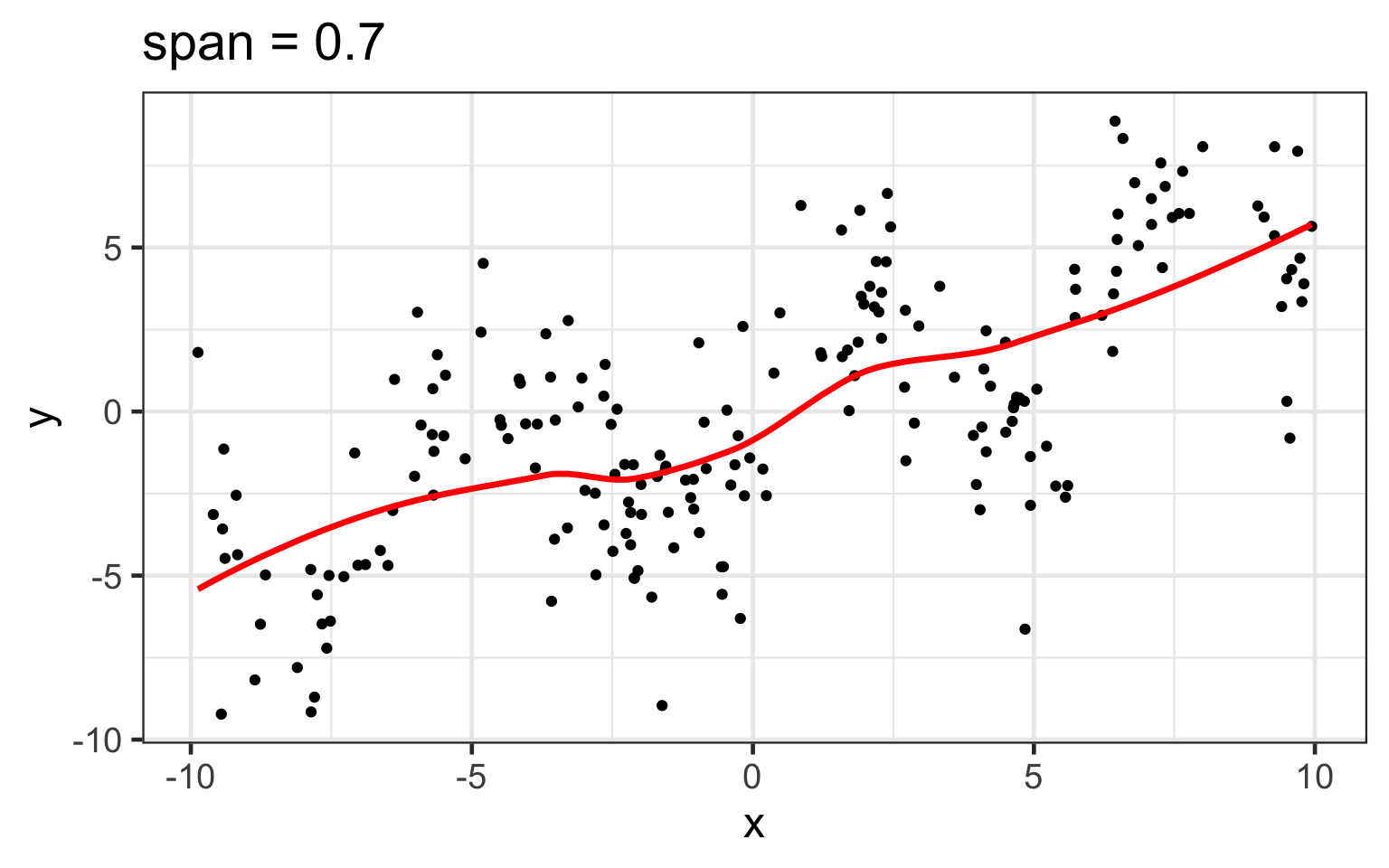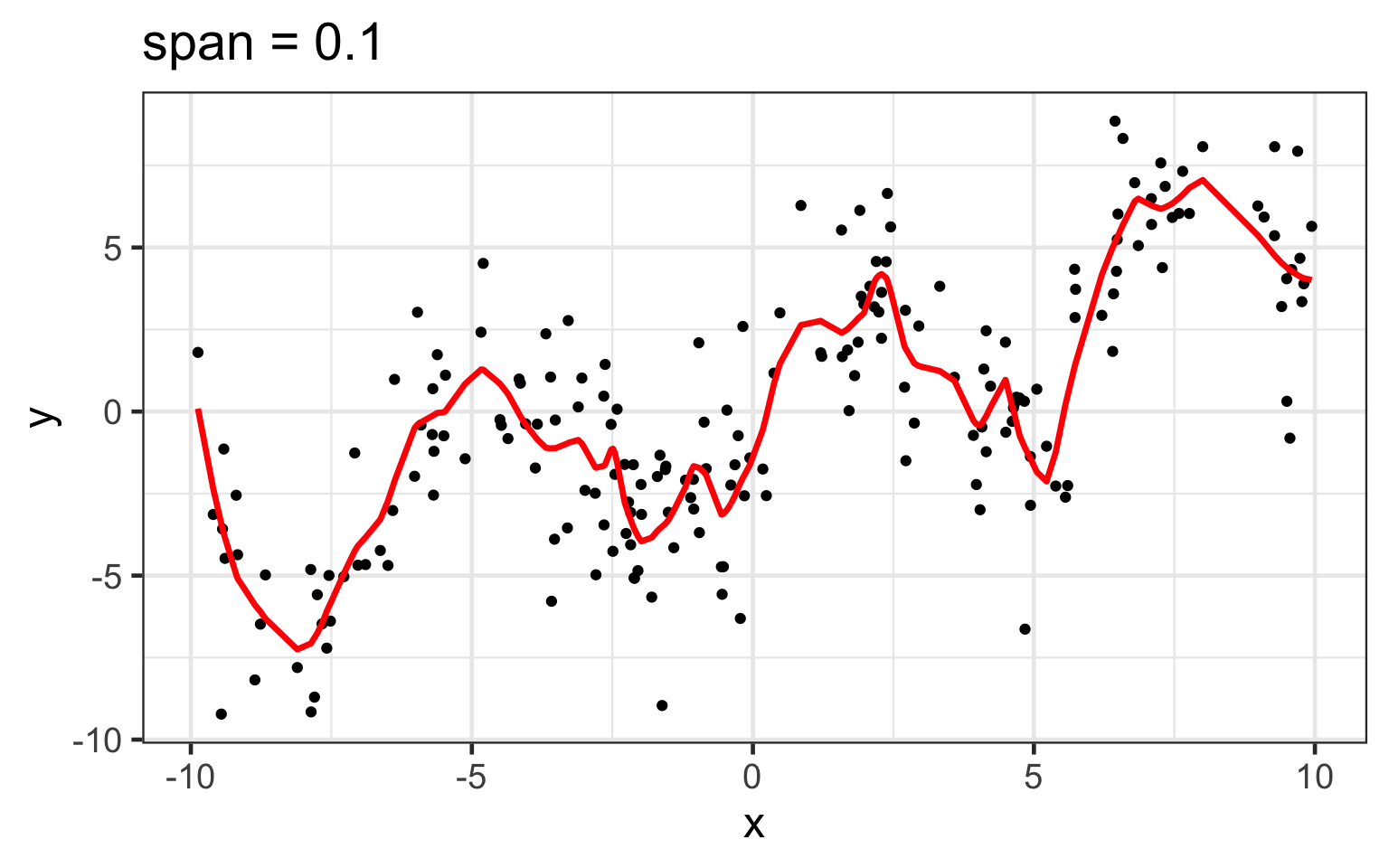
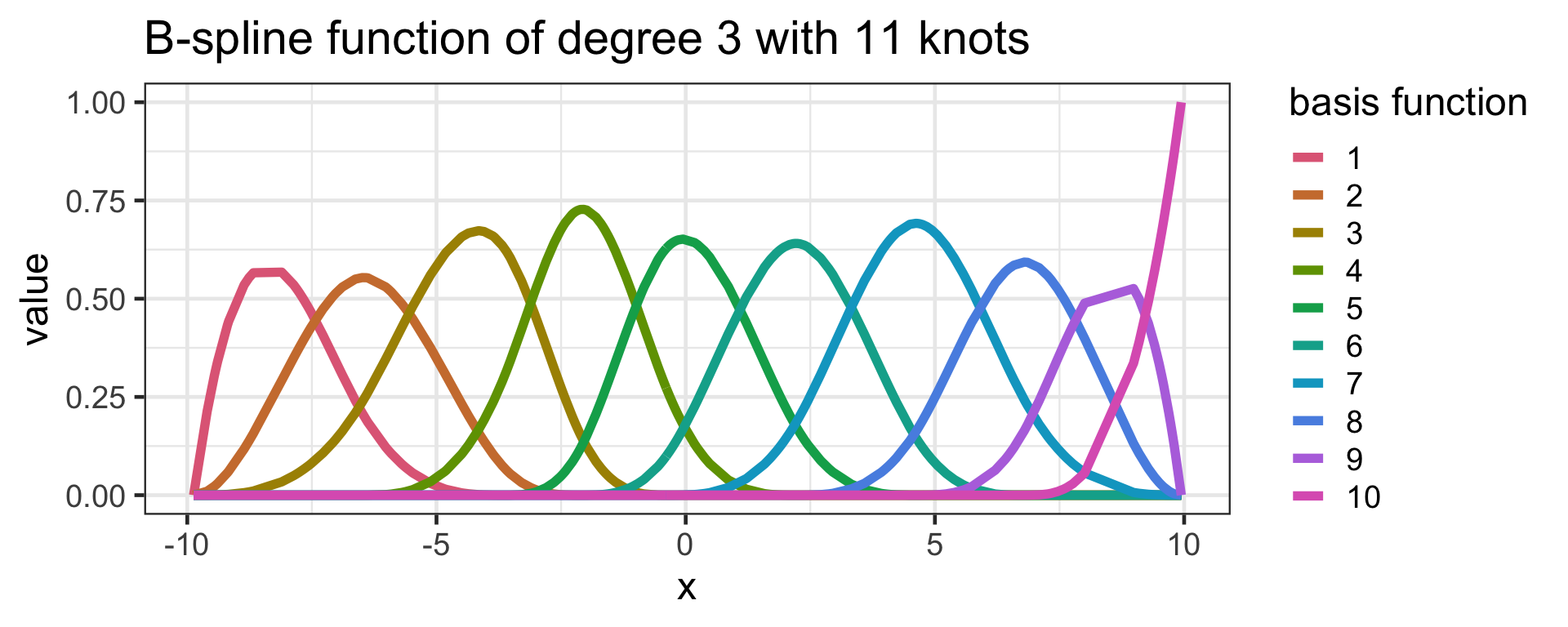
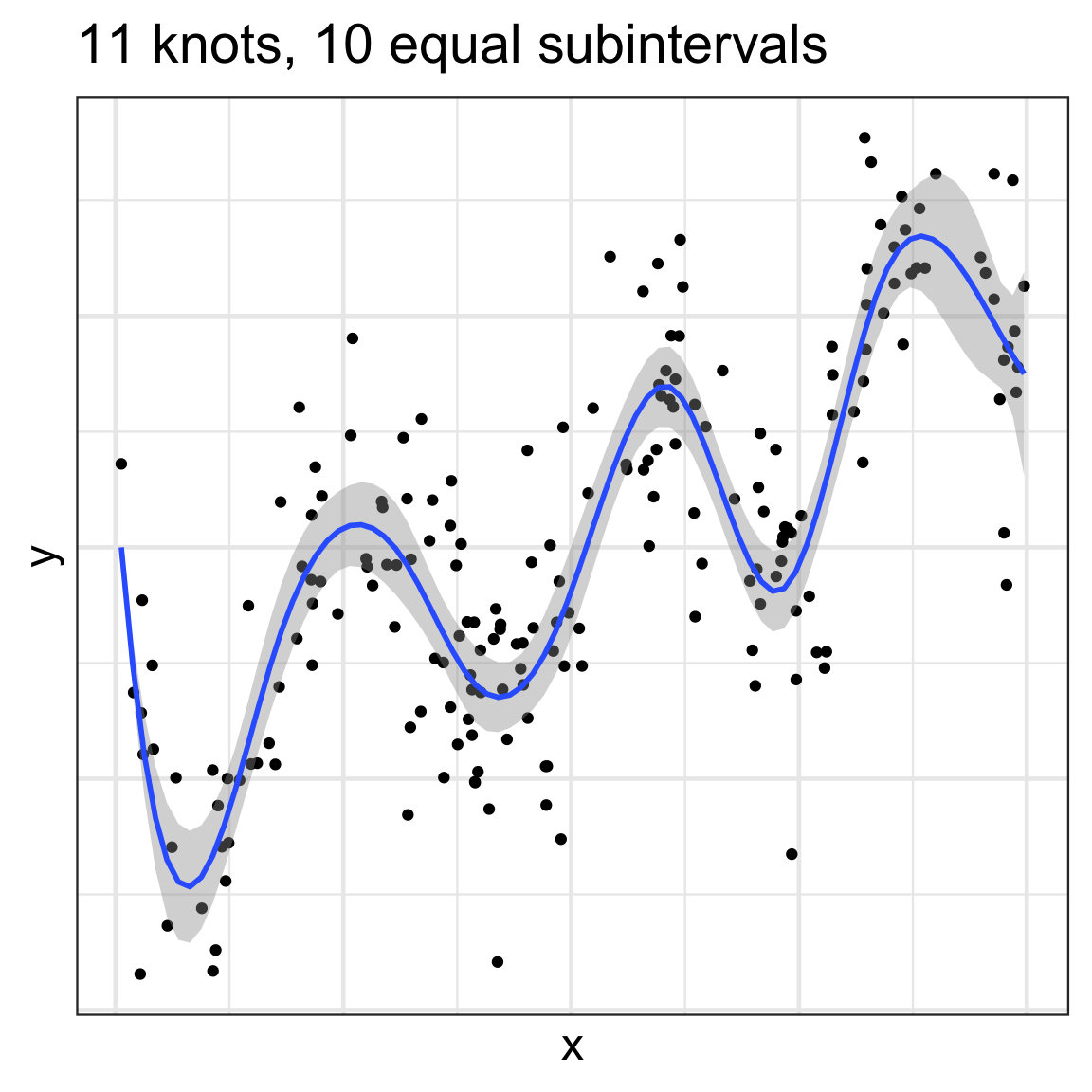
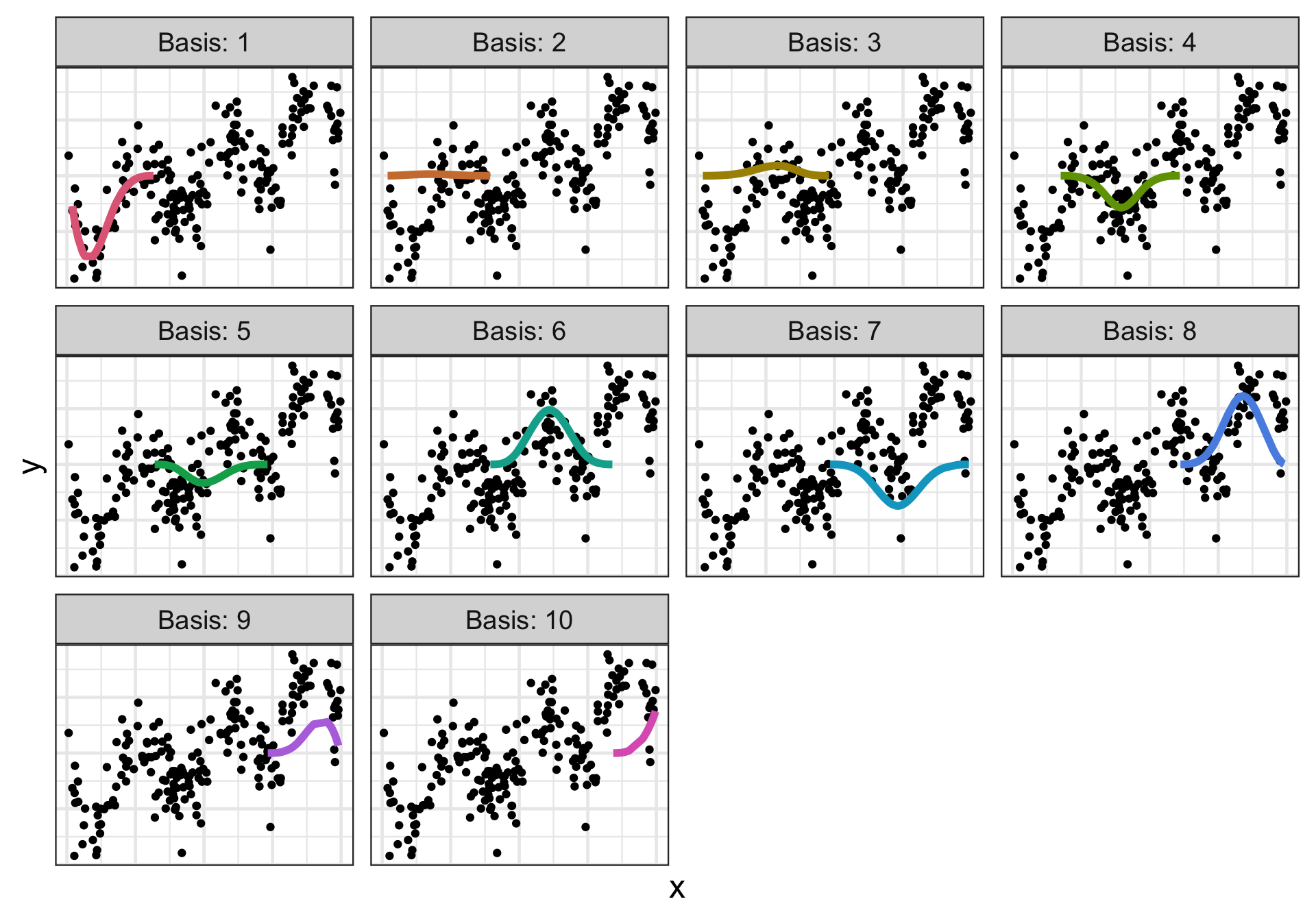
loess works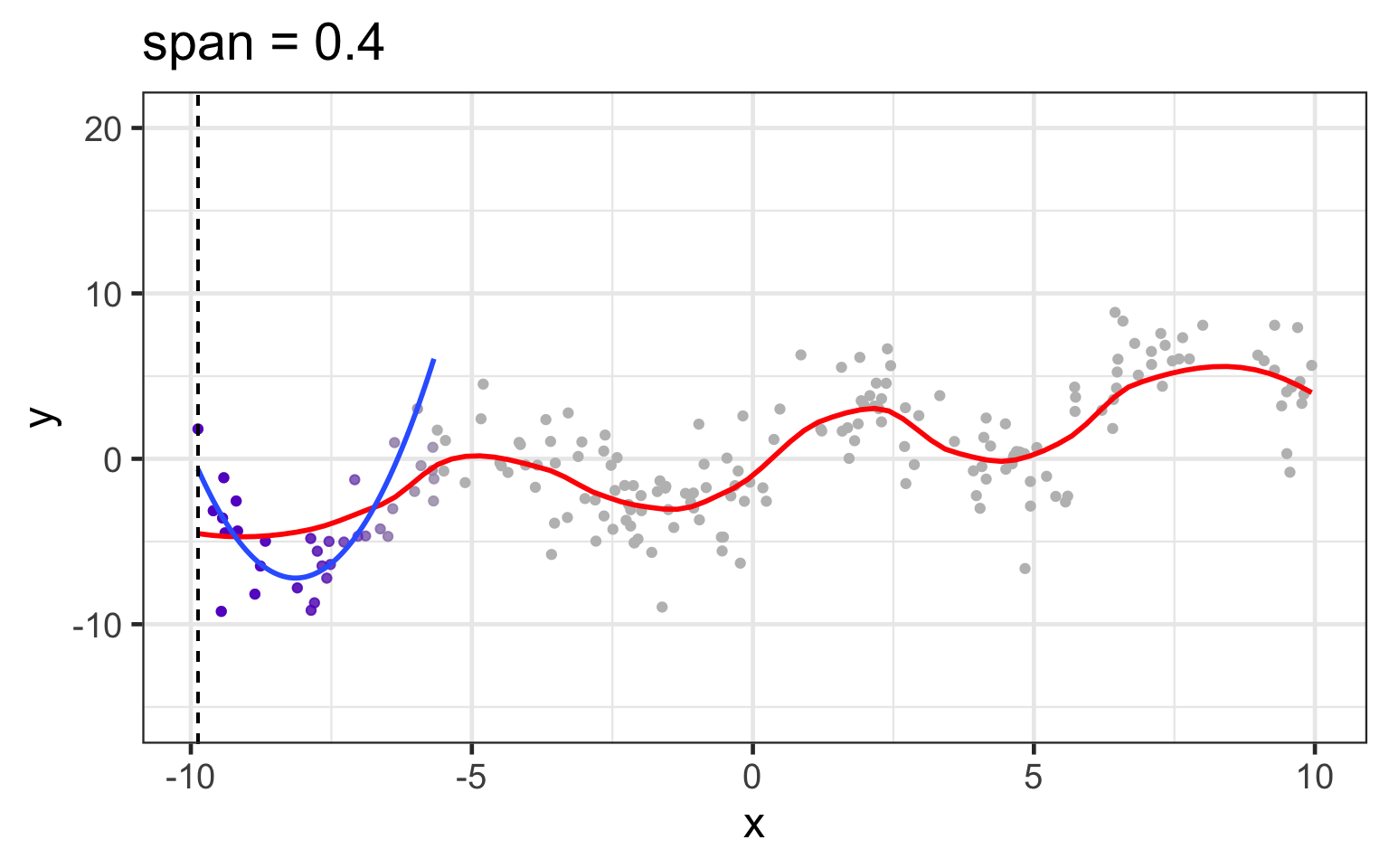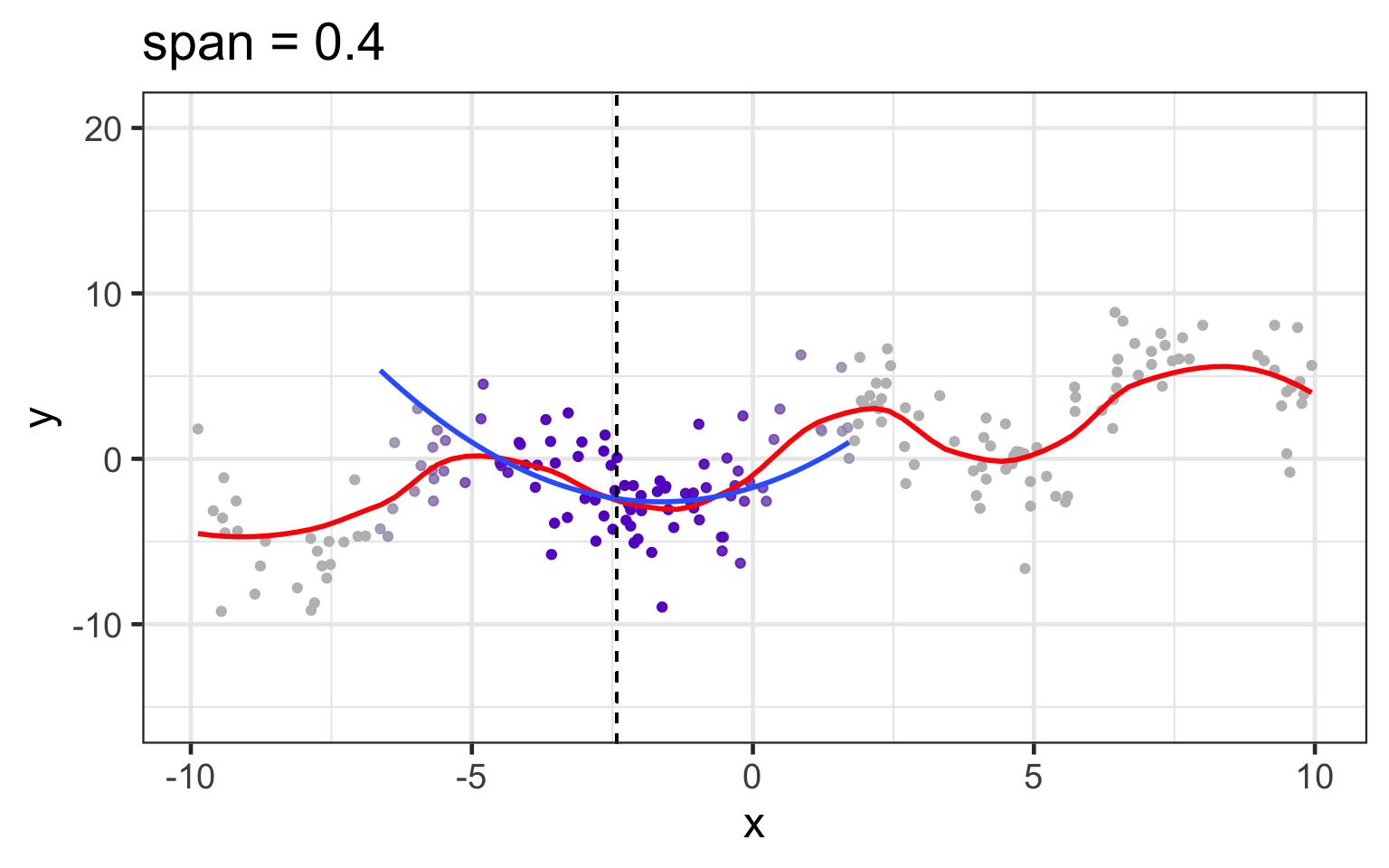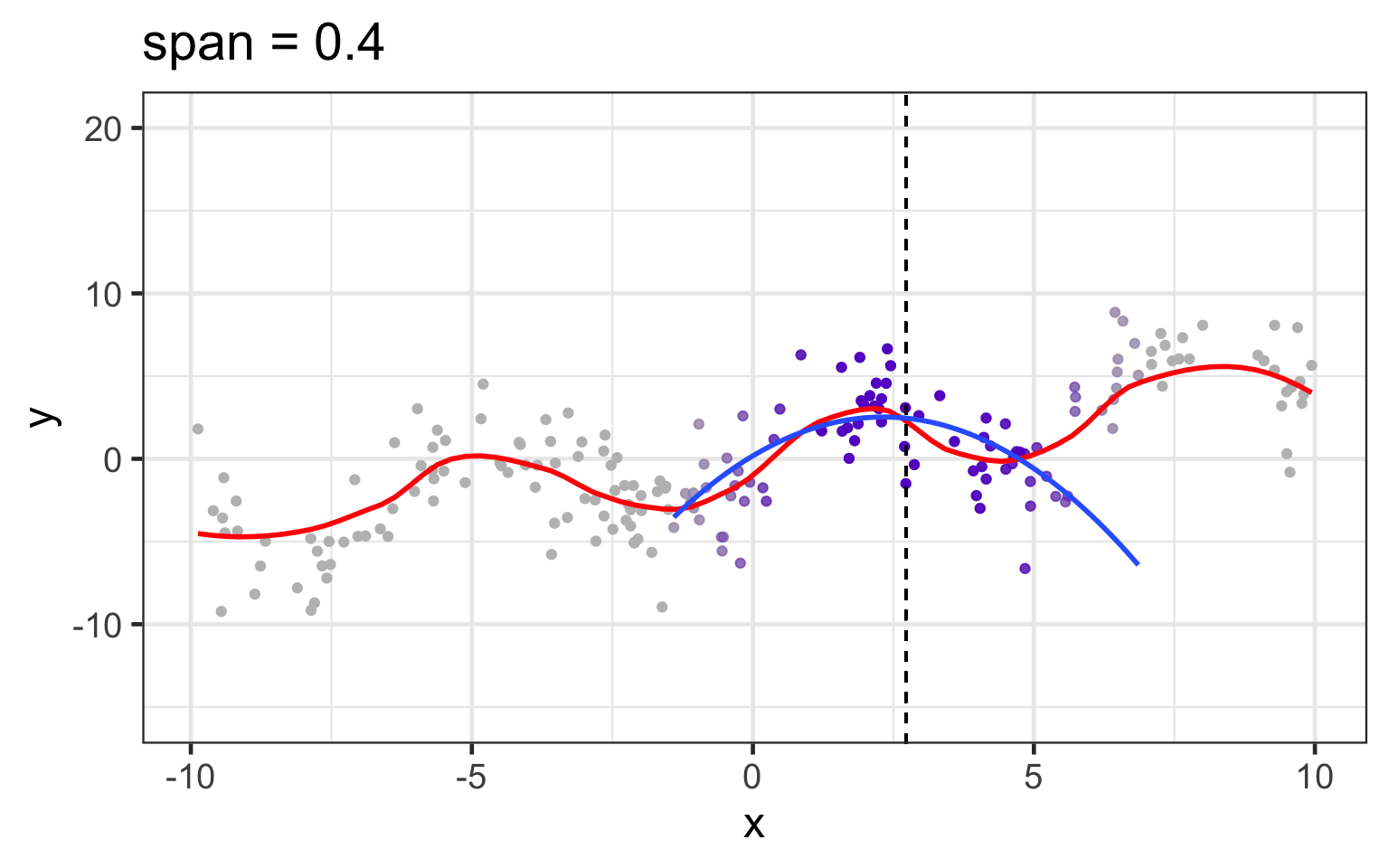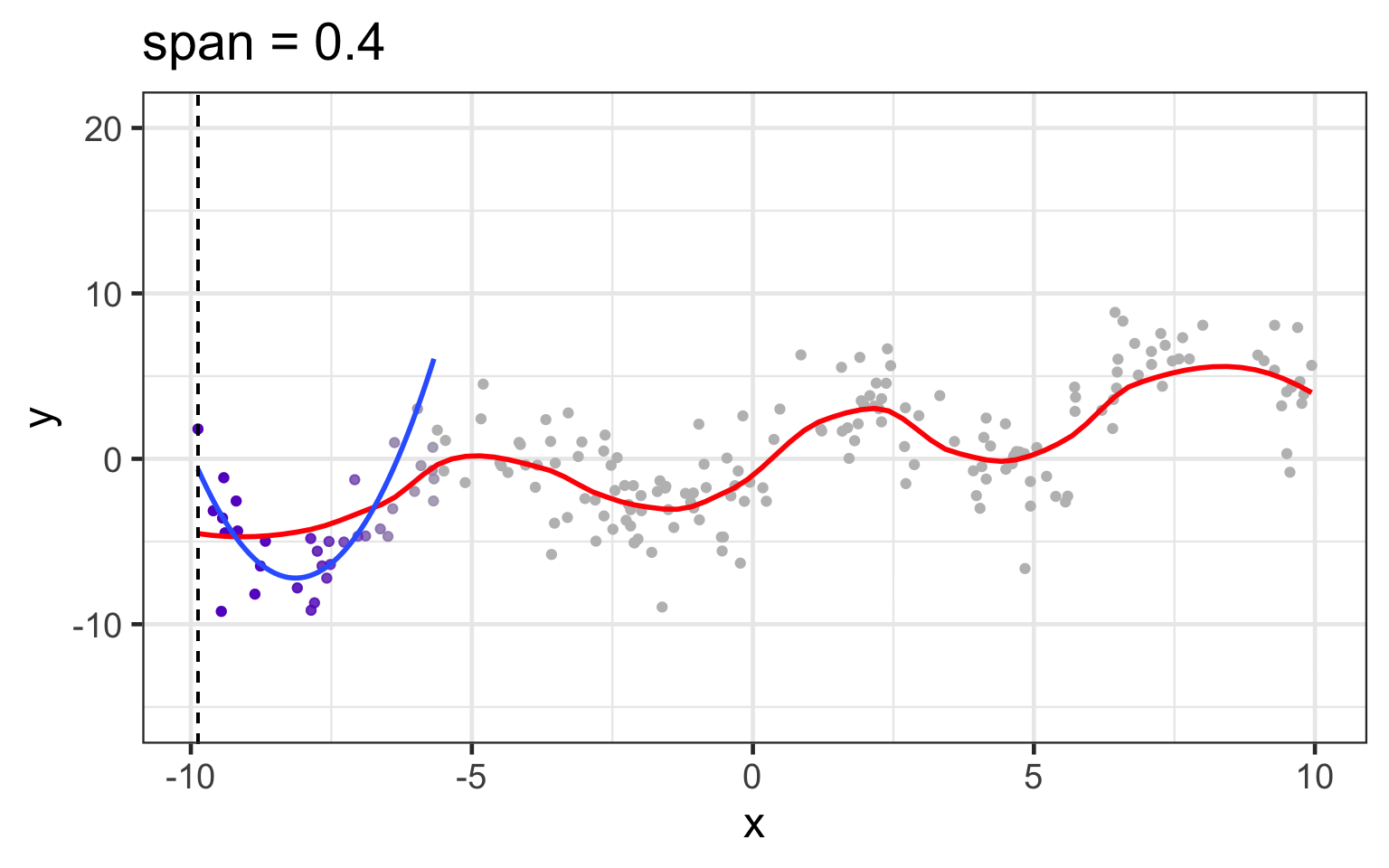

.png)

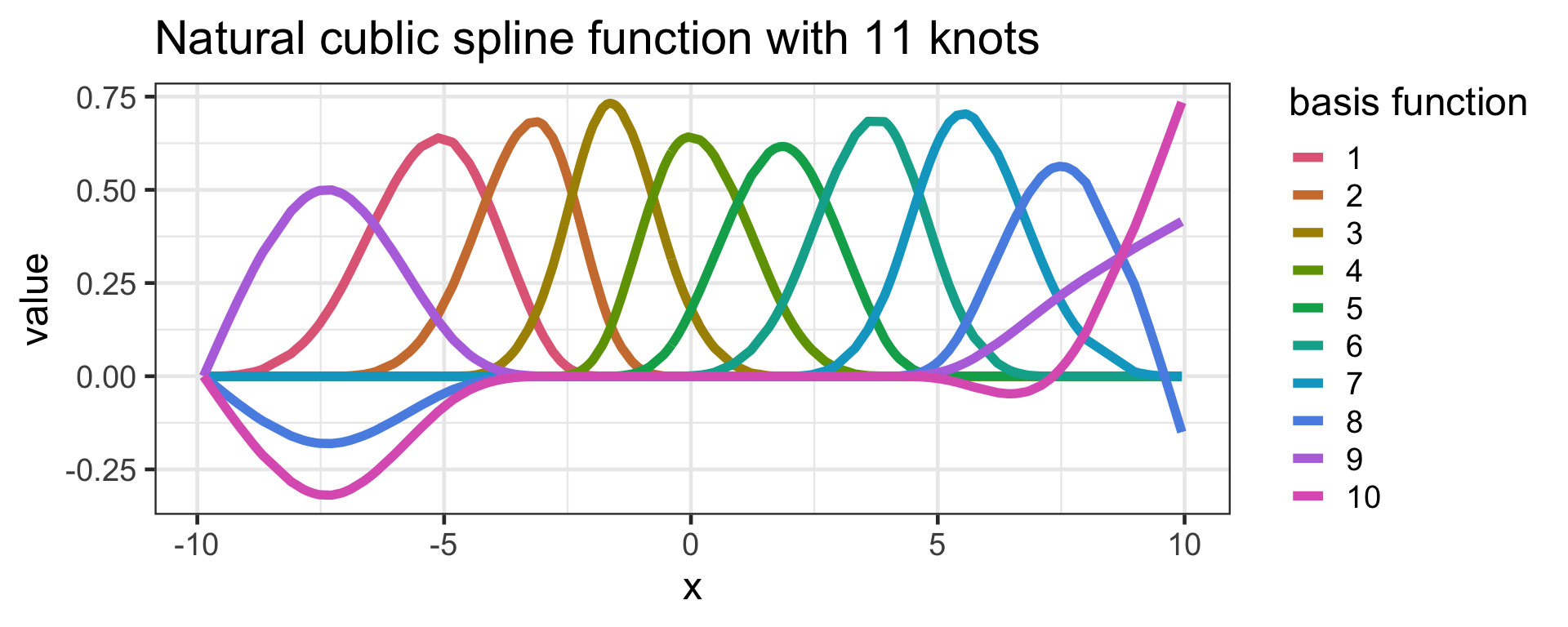
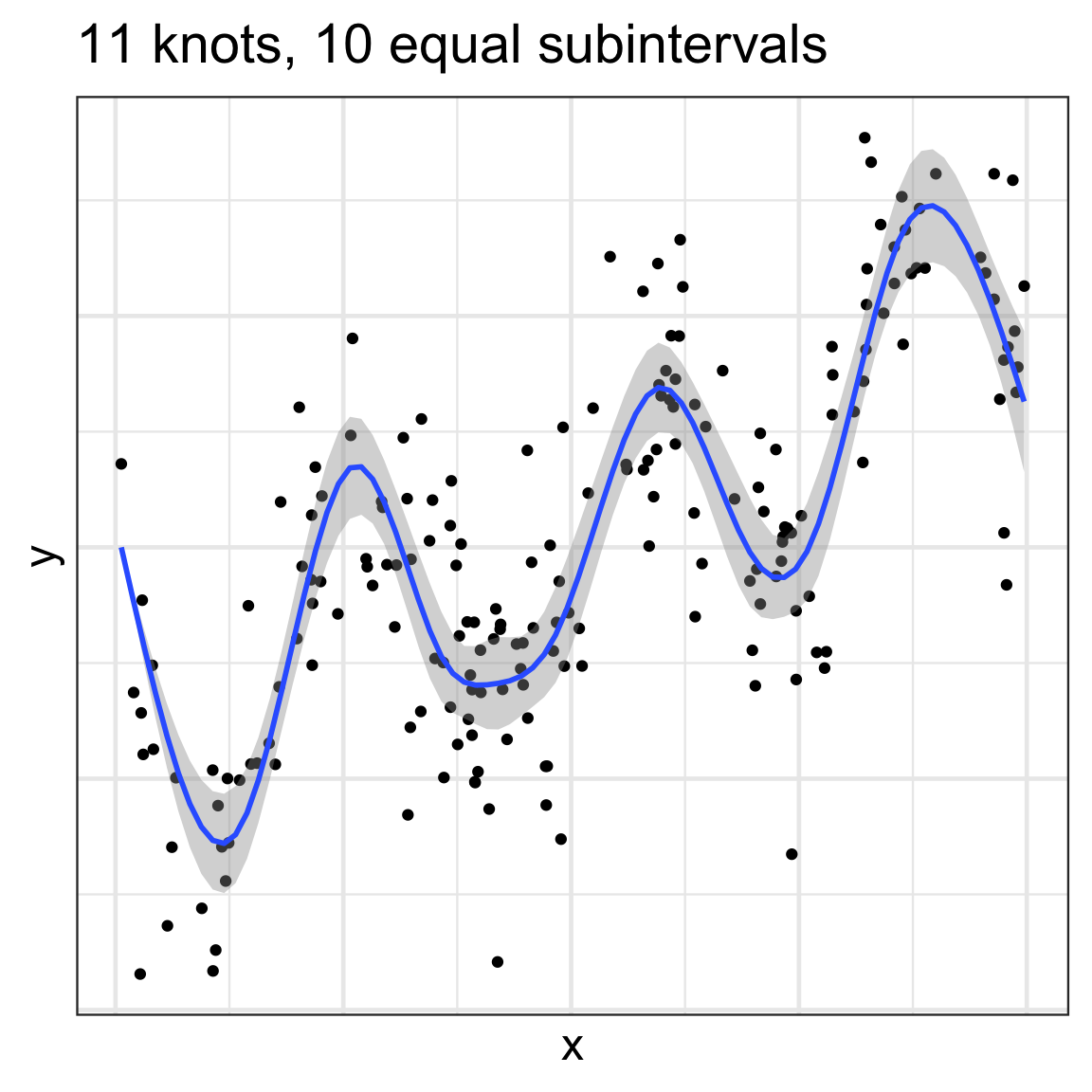

map_dfr(c(0, 2, 3, 8, 14, 48),
~ economics %>%
mutate(
nknot = .x,
nknot_label = paste(nknot, "knots") %>% fct_inorder()
)) %>%
ggplot(aes(date, uempmed, nknot = nknot)) +
geom_point() +
geom_smooth(
method = lm,
formula = y ~ splines::ns(x, df = nknot + 1),
se = FALSE,
colour = "orangered3"
) +
facet_wrap(~ nknot_label) +
ggtitle("Natural cubic splines")

ETC3250/5250 Week 2