ETC5523: Communicating with Data

Statistical model outputs

Lecturer: Emi Tanaka

Department of Econometrics and Business Statistics



Aim

  • Extract information from model objects
  • Understand and create functions in R
  • Understand and apply S3 object-oriented programming in R

Why

  • Working with model objects is necessary for you to get the information you need for communication
  • These concepts will be helpful later when we start developing R-packages

📈 Statistical models

  • All models are approximations of the unknown data generating process
  • How good of an approximation depends on the collected data and the model choice

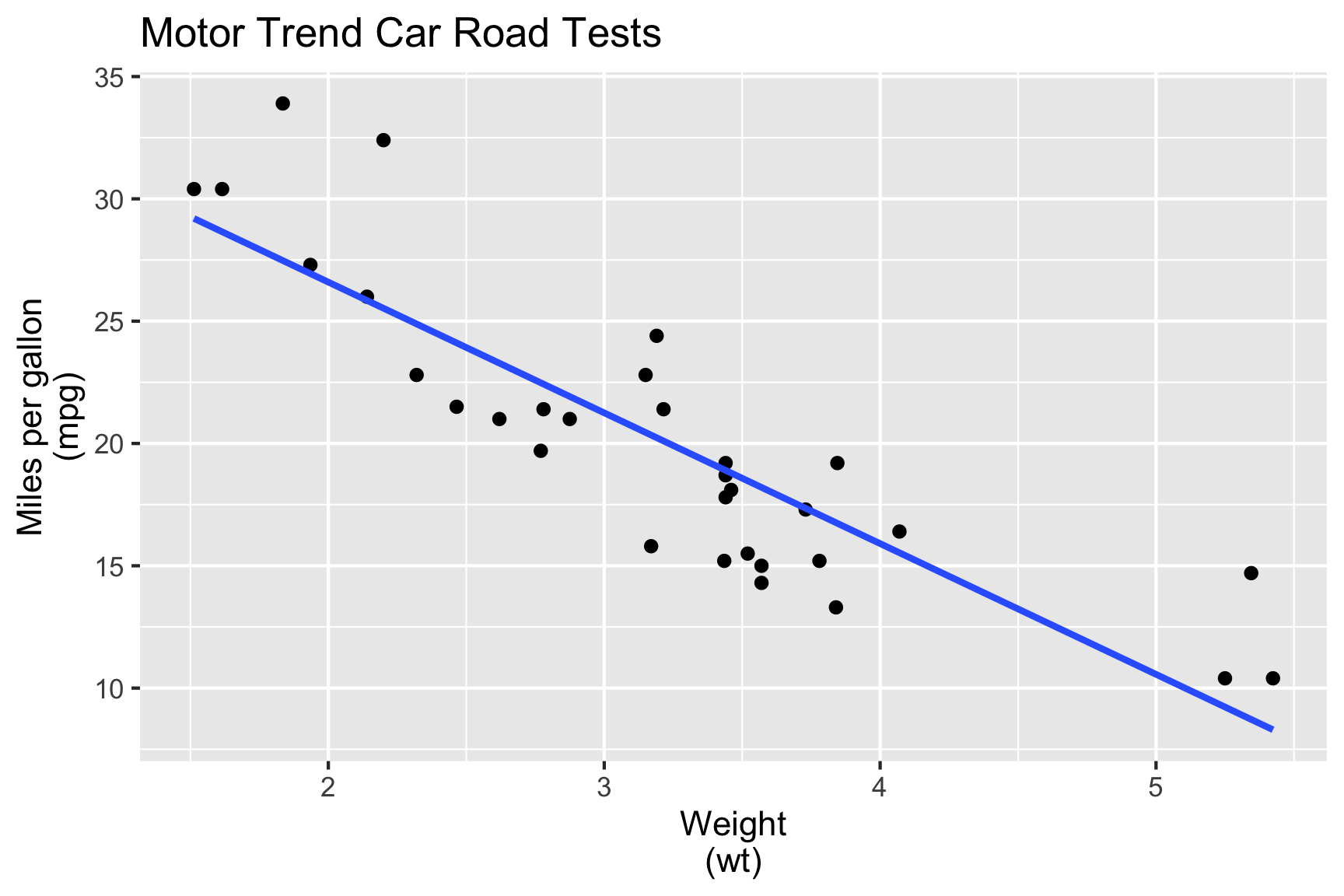
🎯 Characterise mpg in terms of wt.

  • We fit the model:

\[\texttt{mpg}_i = \beta_0 + \beta_1\texttt{wt}_i + e_i\]

Parameter details
  • \(\texttt{mpg}_i\) is the miles per gallon of the \(i\)-th car,
  • \(\texttt{wt}_i\) is the weight of the \(i\)-th car,
  • \(\beta_0\) is the intercept,
  • \(\beta_1\) is the slope, and
  • \(e_i\) is random error, usually assumed \(e_i \sim NID(0, \sigma^2)\)

Fitting linear models in R

\[\texttt{mpg}_i = \beta_0 + \beta_1\texttt{wt}_i + e_i\]

In R we fit this as

fit <- lm(mpg ~ wt, data = mtcars)

which is the same as

fit <- lm(mpg ~ 1 + wt, data = mtcars)
fit

Call:
lm(formula = mpg ~ 1 + wt, data = mtcars)

Coefficients:
(Intercept)           wt  
     37.285       -5.344

\(\hat{\beta}_0 = 37.285\) and \(\hat{\beta}_1 = -5.344\)

ℹ️ Extracting information from the fitted model

  • When you fit a model, there would be a number of information you will be interested in extracting from the fit including:
    • the model parameter estimates,
    • model-related summary statistics, e.g. \(R^2\), AIC and BIC,
    • model-related values, e.g. residuals, fitted values and predictions.
  • So how do you extract these values from the fit?
  • What does fit even contain?

ℹ️ Extracting information from the fitted model

str(fit)
List of 12
 $ coefficients : Named num [1:2] 37.29 -5.34
  ..- attr(*, "names")= chr [1:2] "(Intercept)" "wt"
 $ residuals    : Named num [1:32] -2.28 -0.92 -2.09 1.3 -0.2 ...
  ..- attr(*, "names")= chr [1:32] "Mazda RX4" "Mazda RX4 Wag" "Datsun 710" "Hornet 4 Drive" ...
 $ effects      : Named num [1:32] -113.65 -29.116 -1.661 1.631 0.111 ...
  ..- attr(*, "names")= chr [1:32] "(Intercept)" "wt" "" "" ...
 $ rank         : int 2
 $ fitted.values: Named num [1:32] 23.3 21.9 24.9 20.1 18.9 ...
  ..- attr(*, "names")= chr [1:32] "Mazda RX4" "Mazda RX4 Wag" "Datsun 710" "Hornet 4 Drive" ...
 $ assign       : int [1:2] 0 1
 $ qr           :List of 5
  ..$ qr   : num [1:32, 1:2] -5.657 0.177 0.177 0.177 0.177 ...
  .. ..- attr(*, "dimnames")=List of 2
  .. .. ..$ : chr [1:32] "Mazda RX4" "Mazda RX4 Wag" "Datsun 710" "Hornet 4 Drive" ...
  .. .. ..$ : chr [1:2] "(Intercept)" "wt"
  .. ..- attr(*, "assign")= int [1:2] 0 1
  ..$ qraux: num [1:2] 1.18 1.05
  ..$ pivot: int [1:2] 1 2
  ..$ tol  : num 1e-07
  ..$ rank : int 2
  ..- attr(*, "class")= chr "qr"
 $ df.residual  : int 30
 $ xlevels      : Named list()
 $ call         : language lm(formula = mpg ~ 1 + wt, data = mtcars)
 $ terms        :Classes 'terms', 'formula'  language mpg ~ 1 + wt
  .. ..- attr(*, "variables")= language list(mpg, wt)
  .. ..- attr(*, "factors")= int [1:2, 1] 0 1
  .. .. ..- attr(*, "dimnames")=List of 2
  .. .. .. ..$ : chr [1:2] "mpg" "wt"
  .. .. .. ..$ : chr "wt"
  .. ..- attr(*, "term.labels")= chr "wt"
  .. ..- attr(*, "order")= int 1
  .. ..- attr(*, "intercept")= int 1
  .. ..- attr(*, "response")= int 1
  .. ..- attr(*, ".Environment")=<environment: R_GlobalEnv> 
  .. ..- attr(*, "predvars")= language list(mpg, wt)
  .. ..- attr(*, "dataClasses")= Named chr [1:2] "numeric" "numeric"
  .. .. ..- attr(*, "names")= chr [1:2] "mpg" "wt"
 $ model        :'data.frame':  32 obs. of  2 variables:
  ..$ mpg: num [1:32] 21 21 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 ...
  ..$ wt : num [1:32] 2.62 2.88 2.32 3.21 3.44 ...
  ..- attr(*, "terms")=Classes 'terms', 'formula'  language mpg ~ 1 + wt
  .. .. ..- attr(*, "variables")= language list(mpg, wt)
  .. .. ..- attr(*, "factors")= int [1:2, 1] 0 1
  .. .. .. ..- attr(*, "dimnames")=List of 2
  .. .. .. .. ..$ : chr [1:2] "mpg" "wt"
  .. .. .. .. ..$ : chr "wt"
  .. .. ..- attr(*, "term.labels")= chr "wt"
  .. .. ..- attr(*, "order")= int 1
  .. .. ..- attr(*, "intercept")= int 1
  .. .. ..- attr(*, "response")= int 1
  .. .. ..- attr(*, ".Environment")=<environment: R_GlobalEnv> 
  .. .. ..- attr(*, "predvars")= language list(mpg, wt)
  .. .. ..- attr(*, "dataClasses")= Named chr [1:2] "numeric" "numeric"
  .. .. .. ..- attr(*, "names")= chr [1:2] "mpg" "wt"
 - attr(*, "class")= chr "lm"

ℹ️ Extracting information from the fitted model

Accessing model parameter estimates:

fit$coefficients
(Intercept)          wt 
  37.285126   -5.344472 
# OR using
coef(fit)
(Intercept)          wt 
  37.285126   -5.344472

This gives us the estimates of \(\beta_0\) and \(\beta_1\).

But what about \(\sigma^2\)? Recall \(e_i \sim NID(0, \sigma^2)\).

sigma(fit)^2
[1] 9.277398

ℹ️ Extracting information from the fitted model

You can also get a summary of the model object:

summary(fit)

Call:
lm(formula = mpg ~ 1 + wt, data = mtcars)

Residuals:
    Min      1Q  Median      3Q     Max 
-4.5432 -2.3647 -0.1252  1.4096  6.8727 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  37.2851     1.8776  19.858  < 2e-16 ***
wt           -5.3445     0.5591  -9.559 1.29e-10 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.046 on 30 degrees of freedom
Multiple R-squared:  0.7528,    Adjusted R-squared:  0.7446 
F-statistic: 91.38 on 1 and 30 DF,  p-value: 1.294e-10

So how do I extract these summary values out?

Model objects to tidy data

broom::tidy(fit)
# A tibble: 2 × 5
  term        estimate std.error statistic  p.value
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)    37.3      1.88      19.9  8.24e-19
2 wt             -5.34     0.559     -9.56 1.29e-10
broom::glance(fit)
# A tibble: 1 × 12
  r.squared adj.r.squa…¹ sigma stati…²  p.value    df logLik   AIC   BIC devia…³
      <dbl>        <dbl> <dbl>   <dbl>    <dbl> <dbl>  <dbl> <dbl> <dbl>   <dbl>
1     0.753        0.745  3.05    91.4 1.29e-10     1  -80.0  166.  170.    278.
# … with 2 more variables: df.residual <int>, nobs <int>, and abbreviated
#   variable names ¹​adj.r.squared, ²​statistic, ³​deviance
# ℹ Use `colnames()` to see all variable names
broom::augment(fit)
# A tibble: 32 × 9
   .rownames           mpg    wt .fitted .resid   .hat .sigma   .cooksd .std.r…¹
   <chr>             <dbl> <dbl>   <dbl>  <dbl>  <dbl>  <dbl>     <dbl>    <dbl>
 1 Mazda RX4          21    2.62    23.3 -2.28  0.0433   3.07 0.0133     -0.766 
 2 Mazda RX4 Wag      21    2.88    21.9 -0.920 0.0352   3.09 0.00172    -0.307 
 3 Datsun 710         22.8  2.32    24.9 -2.09  0.0584   3.07 0.0154     -0.706 
 4 Hornet 4 Drive     21.4  3.22    20.1  1.30  0.0313   3.09 0.00302     0.433 
 5 Hornet Sportabout  18.7  3.44    18.9 -0.200 0.0329   3.10 0.0000760  -0.0668
 6 Valiant            18.1  3.46    18.8 -0.693 0.0332   3.10 0.000921   -0.231 
 7 Duster 360         14.3  3.57    18.2 -3.91  0.0354   3.01 0.0313     -1.31  
 8 Merc 240D          24.4  3.19    20.2  4.16  0.0313   3.00 0.0311      1.39  
 9 Merc 230           22.8  3.15    20.5  2.35  0.0314   3.07 0.00996     0.784 
10 Merc 280           19.2  3.44    18.9  0.300 0.0329   3.10 0.000171    0.100 
# … with 22 more rows, and abbreviated variable name ¹​.std.resid
# ℹ Use `print(n = ...)` to see more rows

But how do these functions work?

Functions in

Revise about functions at Learn R

Functions in R

  • Functions can be broken into three components:

    • formals(), the list of arguments,
    • body(), the code inside the function, and
    • environment()1.

  • Functions in R are created using function() with binding to a name using <- or =

Functions in R

f1 <- function(x) sum(x) / length(x)
formals(f1)
$x
body(f1)
sum(x)/length(x)
environment(f1)
<environment: R_GlobalEnv>

Function Example 1

f1 <- function(x) sum(x) / length(x)


x1 <- c(1, 1, 2, 2)
f1(x1)
[1] 1.5

What if there are missing values in the vector or the values are dates?

x2 <- c(1, 1, 2, 2, NA)
f1(x2)
[1] NA
x3 <- as.Date(c("2021-08-04", "2021-08-11"))
f1(x3)
Error in Summary.Date(structure(c(18843, 18850), class = "Date"), na.rm = FALSE): sum not defined for "Date" objects

Function Example 2

f2 <- function(x, na.rm = TRUE) {
  n <- sum(!is.na(x))
  sum(x, na.rm = na.rm) / n
}


f2(x1)
[1] 1.5
f2(x2)
[1] 1.5
f2(x3)
Error in Summary.Date(structure(c(18843, 18850), class = "Date"), na.rm = TRUE): sum not defined for "Date" objects

Function Example 3

f3 <- function(x, na.rm = TRUE) {
  n <- sum(!is.na(x))
  out <- sum(as.numeric(x), na.rm = na.rm) / n 
  if(class(x)=="Date") { 
    return(as.Date(out, 
                   origin = "1970-01-01")) 
  } 
  out
}
f3(x1)
[1] 1.5
f3(x2)
[1] 1.5
f3(x3)
[1] "2021-08-07"
  • What about for another object class?
x4 <- as.POSIXct(c("2021-08-11 18:00", "2021-08-11 20:00"), tz = "UTC")

S3 Object oriented programming (OOP)

  • The S3 system is the most widely used OOP system in R but there are other OOP systems in R, e.g. the S4 system is used for model objects in lme4 R-package, but it will be out of scope for this unit
class(x1)
[1] "numeric"
class(x2)
[1] "numeric"
class(x3)
[1] "Date"
class(x4)
[1] "POSIXct" "POSIXt"

S3 Object oriented programming (OOP)

  • Here I create a generic called f4:
f4 <- function(x, ...) UseMethod("f4")
  • And an associated default method:
f4.default <- function(x, na.rm = TRUE) {
  sum(x, na.rm = na.rm) / sum(!is.na(x))
}
  • And an associated specific method for the Date class:
f4.Date <- function(x, na.rm = TRUE) {
  out <- f4.default(as.numeric(x), na.rm = na.rm)
  as.Date(out, origin = "1970-01-01")
}

S3 Object oriented programming (OOP)

f4(x1)
[1] 1.5
f4(x2)
[1] 1.5
f4(x3)
[1] "2021-08-07"
class(x4)
[1] "POSIXct" "POSIXt" 
f4.POSIXct <- function(x, na.rm = TRUE) {
  out <- f4.default(as.numeric(x), na.rm = na.rm)
  as.POSIXct(out, 
             tz = attr(x, "tzone"), 
             origin = "1970-01-01")
}
f4(x4)
[1] "2021-08-11 19:00:00 UTC"

S3 Object oriented programming (OOP)

  • A method is created by using the form generic.class.
  • When using a method for class, you can omit the .class from the function.
  • E.g. f4(x4) is the same as f4.POSIXct(x4) since the class of x4 is POSIXct (and POSIXt).
  • But notice f4.numeric doesn’t exist, instead there is f4.default.
  • default is a special class and when a generic doesn’t have a method for the corresponding class, it falls back to generic.default

Working with model objects
in

Modelling in R

  • There are many R-packages that fit all kinds of models, e.g. 
    • mgcv fits generalized additive models,
    • rstanarm fits Bayesian regression models using Stan, and
    • fable fits forecast models,
    • many other contributions by the community.
  • There are a lot of new R-packages contributed — some implementing the latest research results.
  • This means that if you want to use the state-of-the-art research, then you need to work with model objects beyond the standard lm and glm.

Example with Bayesian regression

library(rstanarm)
fit_stan <- stan_lm(mpg ~ 1 + wt, data = mtcars,
                    prior = R2(0.7528, what = "mean"))

SAMPLING FOR MODEL 'lm' NOW (CHAIN 1).
Chain 1: 
Chain 1: Gradient evaluation took 5.2e-05 seconds
Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.52 seconds.
Chain 1: Adjust your expectations accordingly!
Chain 1: 
Chain 1: 
Chain 1: Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 1: Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 1: Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 1: Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 1: Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 1: Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 1: Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 1: Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 1: Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 1: Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 1: Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 1: Iteration: 2000 / 2000 [100%]  (Sampling)
Chain 1: 
Chain 1:  Elapsed Time: 0.168063 seconds (Warm-up)
Chain 1:                0.246159 seconds (Sampling)
Chain 1:                0.414222 seconds (Total)
Chain 1: 

SAMPLING FOR MODEL 'lm' NOW (CHAIN 2).
Chain 2: 
Chain 2: Gradient evaluation took 1e-05 seconds
Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.1 seconds.
Chain 2: Adjust your expectations accordingly!
Chain 2: 
Chain 2: 
Chain 2: Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 2: Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 2: Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 2: Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 2: Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 2: Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 2: Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 2: Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 2: Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 2: Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 2: Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 2: Iteration: 2000 / 2000 [100%]  (Sampling)
Chain 2: 
Chain 2:  Elapsed Time: 0.183966 seconds (Warm-up)
Chain 2:                0.121704 seconds (Sampling)
Chain 2:                0.30567 seconds (Total)
Chain 2: 

SAMPLING FOR MODEL 'lm' NOW (CHAIN 3).
Chain 3: 
Chain 3: Gradient evaluation took 1.1e-05 seconds
Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 0.11 seconds.
Chain 3: Adjust your expectations accordingly!
Chain 3: 
Chain 3: 
Chain 3: Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 3: Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 3: Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 3: Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 3: Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 3: Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 3: Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 3: Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 3: Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 3: Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 3: Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 3: Iteration: 2000 / 2000 [100%]  (Sampling)
Chain 3: 
Chain 3:  Elapsed Time: 0.193221 seconds (Warm-up)
Chain 3:                0.112252 seconds (Sampling)
Chain 3:                0.305473 seconds (Total)
Chain 3: 

SAMPLING FOR MODEL 'lm' NOW (CHAIN 4).
Chain 4: 
Chain 4: Gradient evaluation took 1e-05 seconds
Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0.1 seconds.
Chain 4: Adjust your expectations accordingly!
Chain 4: 
Chain 4: 
Chain 4: Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 4: Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 4: Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 4: Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 4: Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 4: Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 4: Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 4: Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 4: Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 4: Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 4: Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 4: Iteration: 2000 / 2000 [100%]  (Sampling)
Chain 4: 
Chain 4:  Elapsed Time: 0.131779 seconds (Warm-up)
Chain 4:                0.120024 seconds (Sampling)
Chain 4:                0.251803 seconds (Total)
Chain 4: 
broom::tidy(fit_stan)
Error in warn_on_stanreg(x): The supplied model object seems to be outputted from the rstanarm package. Tidiers for mixed model output now live in the broom.mixed package.

Huh?

S3 Object classes

  • So how do you find out the functions that work with model objects?
  • First notice the class of the object fit:
class(fit)
[1] "lm"
  • The methods associated with this can be found using:
methods(class = "lm")
 [1] add1           alias          anova          augment        case.names    
 [6] coerce         confint        cooks.distance deviance       dfbeta        
[11] dfbetas        drop1          dummy.coef     effects        extractAIC    
[16] family         formula        fortify        glance         hatvalues     
[21] influence      initialize     kappa          labels         logLik        
[26] model.frame    model.matrix   nobs           plot           predict       
[31] print          proj           qqnorm         qr             residuals     
[36] rstandard      rstudent       show           simulate       slotsFromS3   
[41] summary        tidy           variable.names vcov          
see '?methods' for accessing help and source code

Where is coef()?

Case study broom::tidy

class(fit_stan)
[1] "stanreg" "glm"     "lm"     
broom::tidy
function (x, ...) 
{
    UseMethod("tidy")
}
<bytecode: 0x7fcf4cb44ae0>
<environment: namespace:generics>

There is no tidy.stanreg method so uses the broom:::tidy.glm instead.

Case study broom::tidy

library(broom)

tidy.stanreg <- function(x, ...) {
  est <- x$coefficients
  tibble(term = names(est), 
         estimate = unname(est),
         std.error = x$ses)
}

tidy(fit_stan)
# A tibble: 2 × 3
  term        estimate std.error
  <chr>          <dbl>     <dbl>
1 (Intercept)    30.4      1.34 
2 wt             -3.20     0.347

Working with model objects

  • Is this only for R though?
  • How do you work with model objects in general?

Python

import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression
x = np.array(r.mtcars['wt']).reshape(-1, 1)
y = np.array(r.mtcars['mpg'])
model = LinearRegression().fit(x, y)

[model.intercept_, model.coef_]
[37.28512616734204, array([-5.34447157])]

(Intercept)          wt 
  37.285126   -5.344472

Week 5A Lesson

Summary

  • Model objects are usually a list returning multiple output from the model fit
  • When working with model objects, check the object structure and find the methods associated with it (and of course check the documentation)
  • You should be able to work (or at least know how to get started) with all sort of model objects
  • We revised how to create functions in R
  • We applied S3 object-oriented programming in R

Resources

ETC5523 Week 5A